Introduction
Many real world problems are described by appropriate sets of differential equations which can be developed as models. These model equations are commonly differential equations which can either be linear or nonlinear. Since many of them defy analytic solutions, numerical techniques are often resorted to. Hence understanding the basic conservation laws that lead to the formulation of such problems in addition to the accompanying fluxes are required in order to offer the correct interpretation of the computed results. If however the model is found inadequate and fails to reproduce physically meaningful results or is not in consonance with the physics of the problem, then the problem formulation is revisited based on the information gathered.
Developing accurate numerical techniques that enhance this process requires an ongoing development of new ideas and techniques which can effectively provide accurate numerical solutions.in affordable computing times. From a theoretical point of view, all the conservation laws that describe physical systems lead to fluxes of the quantities conserved; for example, momentum, mass and energy fluxes. To better understand these equations, we need measurable variables such as concentration, pressure, temperature etc. This requires the use of constitutive equations which relate the fluxes to the gradient of scalar being transported. Examples of such equation are the Ficks, Fourier and Newton’s law of cooling. Once they are substituted into the governing partial differential equations, the final form of such equations are obtained in terms of measurable quantities.
Partial differential equations by their very nature deal with continuous functions and must therefore have to be discretized in space and time to arrive at numerical solutions. Discretization results in a system of ordinary differential equations (ODE), which for real world application may comprise hundreds of evolution equations that must be handled numerically. There are numerous methods for achieving this objective. Going into this is way beyond the purpose of this paper. For the purposes of the work described herein we deviate from the classical boundary element (BEM) approach by adopting two types of domain –discretized integral formulation. It is found that the resulting system of discrete equation not possess ‘local support’ as if found in finite element method (FEM) formulation but in addition possess slender coefficient matrices which are easier to handle numerically unlike the square fully populated ones that result from classical application.
Mathematical formulation
Fourth-order boundary value problems including biharmonic differential equations are of huge significance due to their several applications in such areas as applied physics and engineering. Numerical and analytical techniques have been proposed for the study of such problems (Momani and Noor) [1]. Semi-analytic techniques like the Adomian decomposition techniques including several of its variations have been applied by several authors [2,3]. A ‘non-boundary only’ approach adopted herein circumvents all numerical perplexing issues related to nonlinearity and transient scalar distribution. The integral representation of a coupled system or multiple differential equations is given as [4],
Where the variable k represents the equation numbering system . M is he total number of equations and is a forcing function. Equation (1) is a general representation of the 1-D Poisson equation obtained by decoupling a fourth-order differential equation. The boundary conditions at the two ends of the problem domain can be specified as:
A quasi -linearization of the forcing function over each of the subdomains is initiated via the Taylor series.
The average value of dependent variable over an element at the current iteration level is . Equation (1) becomes:
Where:
We next introduce a weighted residual formulation for equation (3b) within a subdomain (a,b)
We get rid of the second derivative of the dependent variable by integrating equation (4a) twice to obtain:
We define two weighting functions as respectively. Eq. (4a) becomes:
Next we approximate the dependent variable and its spatial derivative within each subdomain by introducing an osculating polynomial
Where the functions are the osculating polynomials. The integral terms in equation (4c) are evaluated to finally give the following kth equation for each subdomain.
Details of the formulation together with the element level coefficient matrices can be found in [4]. A more elegant and robust formulation of the above procedure can be initiated by applying the Green’s second identity to the stationary part of the linear diffusion operator (the so called Laplace operator) to obtain a singular integral equation. We generalize equation (1) to include convection, reaction and transient terms as well as distributed load.
D is the dispersion coefficient, is the dependent variable U is the velocity in the x-direction, represents an external distributed source and is the rate constant. The auxiliary equation in infinite space is used to derive the free-space Green’s function with a derivative . These together with the Greens second identity are applied to equation (7a) to obtain its integral analog
Lagrange-type interpolations are then applied to the dependent variable and its functions within a genetic element of the problem domain. That is where is the interpolation function with respect to a node j . Introducing the interpolating function into the integral equation yields the element discrete equation
To test the reliability of the above formulations, we choose a fourth order beam-deflection type differential equation whose closed form solution can easily be derived
The order of convergence, the norms of the two formulations are computed with the following formulas:
where is the number of elements. By the same token, norms are defined as
For the purposes of comparison, we shall call the first formulation mod-1 and the latter mod-2. The numerical results are hardly distinguishable for this particular example. However Table 1 shows that mod-2 displays slightly better accuracy and convergence.
| Table 1: Error Norms and Order of Convergence for mod-1 and mod-2. |
| No. Elements |
 norm norm
(mod-1) |
 norm norm
(mod-2) |
Order of Convergence
(mod-1) |
Order of Convergence
(mod-2) |
 norm norm
(mod-1) |
 norm norm
(mod-1) |
| 10 |
.012254 |
.008652 |
1.89752 |
1.99658 |
0.01287 |
.00231 |
| 20 |
.011536 |
.006592 |
1.97321 |
2.00791 |
0.00322 |
.00182 |
| 40 |
.0083712 |
.001229 |
2.01376 |
2.00362 |
.001462 |
.00108 |
We put the robustness of mod-2 to test by solving a beam deflection problem in structural mechanics. A supported beam carries a uniform load of intensity and a tensile force N. The governing fourth order differential equation for the system is given by:
Where EI is the bending rigidity and is the displacement. The boundary conditions are
Changing the variables to converts equation (10a) into
With the following boundary conditions:
We adopt the same decoupling procedure in example (1). Table 2 shows the displacement profiles and their gradients across the beam. Numerical results justify the relative signs of the variable . Identical values are recorded at the middle of the beam.
| Table 2: |
| Coordinates |
Displacement |
Gradient  |
Displacement |
Gradient  |
| 0.1 |
-0.5487e-01 |
-0.4467e+00 |
-0.3269e-01 |
-0.3075e+00 |
| 0.2 |
-0.9072e-01 |
-0.2754e+00 |
-0.6155e-01 |
-0.2666e+00 |
| 0.4 |
-0.1185e+00 |
-0.4476e+00 |
-0.1042e+00 |
-0.1518e+00 |
| 0.5 |
-0.1156e+00 |
0.7466e-01 |
-0.1156e+00 |
-0.7466e-01 |
| 0.65 |
-0.9573e-01 |
0.1850e+00 |
-0.1162e+00 |
-0.7466e-01 |
| 0.8 |
-0.6155e-01 |
0.2666e+00 |
-0.9072e-01 |
0.2754e+00 |
Our next example deals with transient nonlinear fourth-order equation that is described by the following equation:
Where , with initial and boundary conditions:
Equation (11) is decoupled according to:
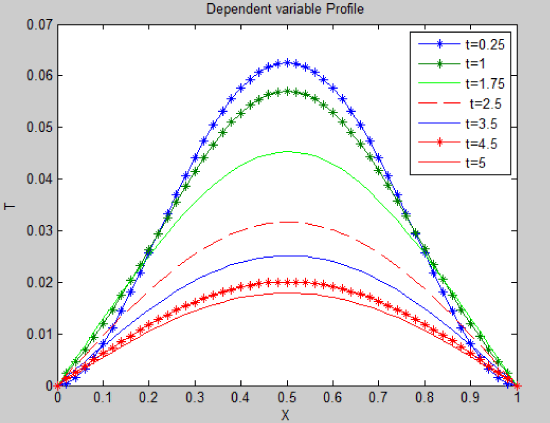
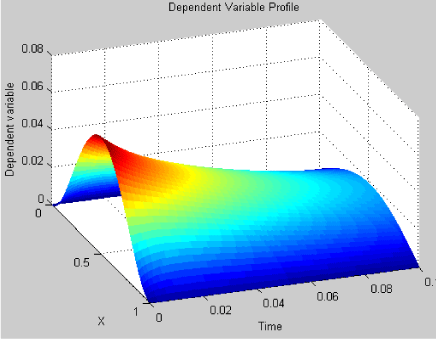
Equation (9) is solved with mod-2 and the nonlinearity is resolved by the Picard algorithm. Figures 1,2, show how the nonlinear initial profile decays with time
Figure 1: Time history of solution profiles.
Figure 2: Decay of transient solution profile.
Conclusion
Two integral formulations based on a boundary-domain interpretation of the boundary element method have been used to numerically solve a Biharmonic and second order coupled linear and nonlinear boundary value problems. Unlike the BEM both methods require that the domain of the problem be discretized in the space-time domain. As a result of this domain- localized integral approach, local support is obtained among the computational nodes, and the resulting coefficient matrix is slender and amenable to numerical manipulation.
 This work is licensed under a Creative Commons Attribution 4.0 International License.
This work is licensed under a Creative Commons Attribution 4.0 International License.

 Save to Mendeley
Save to Mendeley
