Annals of Mathematics and Physics
Determinism and chaos – a story about Big Bang, singularity and the future of mankind
Alexandru Dinu* and Madalin Frunzete
Cite this as
Dinu A, Frunzete M (2023) Determinism and chaos – a story about Big Bang, singularity and the future of mankind. Ann Math Phys 6(1): 041-043. DOI: 10.17352/amp.000075Copyright Licence
© 2023 Dinu A, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.People have always tried to understand and tame the nature around them. It is a well-known fact that the sanest and safe approach from a psychological point of view is to focus on the present moment, the here and now. Nevertheless, we keep looking and living in the past or daydreaming and making predictions about what the future will bring. This paper is looking at this topic trying to unify several perspectives, stemming from a very diverse set of disciplines: biology, genetics, economics and cryptography, which are apparently working in parallel to solve the same problem. They all aim to find a theory of everything, one that can make sense out of chaos, light out of darkness and that can accurately predict the future based on present and past events. The current paper is supposed to inspire researchers to ask themselves tough questions, sometimes completely outside of their comfort zone, that can lead to discoveries with a huge positive impact on us all.
Introduction
Determinism is mankind’s dream. In physics, mathematics, or computer science, a system is considered to be deterministic if it is described by a clear set of rules and equations (i.e., finite difference equations, differential equations, etc.). When one knows the equations which characterize the system and the initial setup/state where the system started, she can determine the state of the system at any moment of interest. Another feature of a deterministic system is that starting from the exact same initial condition and parameters of the system, the same output is exhibited.
Why this fascination with determinism, one may ask? We, human beings, like predictability. Why is that, the researcher might ask next, in the inquisitive spirit of the 5 x WHY technique? There could be multiple explanations and the simple one is usually the closest to the truth (Occam’s razor). We live in a new world, where everything is moving extremely fast and most of us are in a continuous hunt for opportunities, recognition and fame in one form or another. But this was not always like this. A couple of thousands of years back we were still living in the wilderness, in caves, and had to worry about what the next day would bring. In such an environment, predictability was key. No one wanted that a tiger changed its resting place too often or the buffalo herds or bird flocks not to migrate every spring or autumn. If that would have happened, if everything would have been unpredictable in those times, the extinction of the human race would have been on the table [1]. This leads us to the original question: why do we like determinism and things that have a certain sense of order – because it helped us survive until this very moment and the survival instinct always prevails.
Chaos theory
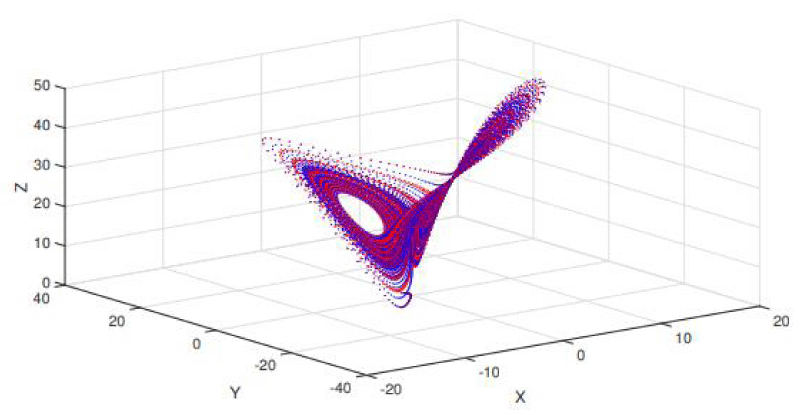
A special class of deterministic systems is the one used in chaos theory. These systems look and are very deterministic at a first glance: if one would know the system used to describe a certain phenomenon and the exact initial conditions, she could predict what follows seconds, minutes, or years later. This brings us to the third aspect mentioned in the title of this paper: the future. People are always interested in predicting with very good accuracy what the future will bring. Information is power and the one that has access to the most up-to-date piece of information has the most chance of success. However, even if one could find all the equations describing the evolution of life or mankind as a whole, the interesting thing is that the initial conditions of such a system (and of a chaotic system, in general) are very difficult to predict and/or find with the desired level of accuracy. An essential characteristic of any chaotic system is that it is extremely sensitive to initial conditions variation. A picture is worth a thousand words, so it is easier to visualize two trajectories obtained from the Lorenz system for two different but very close initial conditions (0.0001 difference) – Figure 1.
The Lorenz system is depicted below (1) and it is making use of a set of three differential equations. This is a good example of a chaotic system that has its origins in the nature surrounding us. It has been discovered by Edward Lorenz, a U.S. meteorologist, who was interested in finding a way to express wind speed and temperature changes and even predict them. The solutions of the differential equations set shown in (1) are moving and evolving around what is called a strange attractor fractal [2]. The set of parameters used in this simulation and which ensure a chaotic behavior occurs is a = 10, b = 8/3, and c = 28. Equation (1) and Figure 1 are included in [2].
The world we live in is constantly preoccupied with the future. A famous quote with different versions around the world is that „if one wants to know what the future will bring, she needs to understand the past”. It has been shown that in the case of a tent map (a discrete chaotic system), used in cryptography, it is wise not to include the initial condition in the binary sequence which is part of the secret key because it can be easily discovered [3]. Today discussed this aspect from the point of view of biology and physics [4]. He is also briefly touching on the famous equation formulated by Albert Einstein E = mc2 and is also referencing recent papers which investigated the recovery of the initial condition (formulated above for tent map and cryptography) in the context of chaotic systems but with a focus on the living world, biology, and physiology [5-6]. Big Bang is another point intensively debated in the literature touched upon in [4] and Torday is mentioning with a certain degree of disappointment that the continuum and the correlation between all life domains and sciences (physics, cosmology, biology, philosophy, etc.) are still to be discovered [8-10]. Deterministic and chaotic systems found their way into the field of economics as well [11-12]. What other field would be more interesting than the one of economics: predicting how the stock market will develop or understanding without a doubt what led to certain recessions or economical crises is of high interest to the entire world and can provide valuable lessons for future generations.
Singularity
In physics, a singularity is a condition in which the spacetime itself would break down catastrophically. The 0 moments of the Universe, the Big Bang, is also considered by recent theories as being a singularity. The concept of singularity is closely related to the idea of observability. Observability is the property of a dynamical system that measures how well information about the history and the internal states of the system can be obtained by having access to the outputs of the system. The singularity manifold is the area where the system is not observable anymore, for a certain state variable. From the point of view of cryptography, the aim is to have a small or no singularity manifold at all.
It is helpful to analyze how the singularity manifold is defined from a mathematical point of view. Equation (2) introduces variables X and Y which correspond to a certain space variable xi for successive iterations.
The observability matrix Oi, defined by (3) for variable xi, is the Jacobian of map Φi.
The singularity manifold is the area in space where the determinant of the observability matrix is 0.
Conclusion
In this paper, we have briefly touched on the topic of singularity and observability in the context of dynamical systems. Dynamical systems and chaos theory started to become prevalent topics in multiple fields like cryptography, economics, and biology. What makes the entire discussion fascinating is that it is linked to an old human interest: what connects all things together? Is there such a thing as a unified theory of everything? Can we reconstruct our past (observability) and can we predict the future? The answer to these questions is still unknown. Nevertheless, we strongly believe that with the recent advances in technology and knowledge, these questions will not remain unanswered for a long time. We also do believe that the answer will come not from a single field of science but will require an inter- and transdisciplinary approach: the unified theory of things can only be discovered if researchers from all branches of science come together and create a novel approach that leverages on the wisdom of the crowds: the pieces of the puzzle are around us, we just need to piece them together.
- Mobbs D, Hagan CC, Dalgleish T, Silston B, Prévost C. The ecology of human fear: survival optimization and the nervous system. Front Neurosci. 2015 Mar 18;9:55. doi: 10.3389/fnins.2015.00055. PMID: 25852451; PMCID: PMC4364301.
- Dinu A, Frunzete M. Singularity, Observability and Statistical Independence in the Context of Chaotic Systems. Mathematics. 2023; 11(2):305. https://doi.org/10.3390/math11020305
- Dinu A, Vlad A. The compound tent map and the connection between Gray codes and the initial condition recovery, Scientific Bulletin – Universitatea Politehnica Bucuresti, A series: Applied Mathematics and Physics. 2014;1.
- Torday JS. The Singularity of nature. Prog Biophys Mol Biol. 2019 Mar;142:23-31. doi: 10.1016/j.pbiomolbio.2018.07.013. Epub 2018 Aug 1. PMID: 30076851.
- Matsuno K. Making biological theory more down to Earth. Prog Biophys Mol Biol. 2013 Sep;113(1):46-56. doi: 10.1016/j.pbiomolbio.2013.03.004. Epub 2013 Apr 2. PMID: 23562478.
- Mazzocchi F. Complexity and the reductionism-holism debate in systems biology. Wiley Interdiscip Rev Syst Biol Med. 2012 Sep-Oct;4(5):413-27. doi: 10.1002/wsbm.1181. Epub 2012 Jul 3. PMID: 22761024.
- Hawking SW, Ellis GFR. The Large-scale Structure of Space-time, University Press, Cambridge. 1973.
- Whitehead AN. Process and Reality. Free Press, New York. 2010.
- Sheldrake R. Science and Spiritual Practices. Counterpoint Press, Berkeley. 2018.
- Smolin L. The Life of the Cosmos. 1999.
- Yusuf A, Qureshi S, Shah SF. Mathematical analysis for an autonomous financial dynamical system via classical and modern fractional operators, Chaos, Solitons & Fractals. 2020; 132:109552; 0960-0779. https://doi.org/10.1016/j.chaos.2019.109552.
- Jahanshahi H, Sajjadi SS, Bekiros S, Aly AA. On the development of variable-order fractional hyperchaotic economic system with a nonlinear model predictive controller, Chaos, Solitons & Fractals. 2021; 144:110698; 0960-0779. https://doi.org/10.1016/j.chaos.2021.110698.
Article Alerts
Subscribe to our articles alerts and stay tuned.
 This work is licensed under a Creative Commons Attribution 4.0 International License.
This work is licensed under a Creative Commons Attribution 4.0 International License.
 Help ?
Help ?

PTZ: We're glad you're here. Please click "create a new query" if you are a new visitor to our website and need further information from us.
If you are already a member of our network and need to keep track of any developments regarding a question you have already submitted, click "take me to my Query."


 Save to Mendeley
Save to Mendeley