J/Ψ (1S) and Ψ (2S) Production in p-p Collisions at E=5.44 TeV

I estimate the differential rapidity cross sections for J/Ψ and Ψ (2S) via pp (proton-proton) collisions at E=510 GeV. The J/Ψ is a standard charm quark and anti-charm quark, c and while Ψ (2S) is a mixed hybrid c meson. For the Ψ (2S) I use the mixed heavy quark hybrid theory, with states approximately 50% standard and 50% hybrid charmonium.

Introduction

This new work on p-p collisions is based on the heavy quark state production formalism in Pb-Pb collisions at $\sqrt{s_{pp}}$ = p-p energy = 5.02 TeV [1].

I use the standard model the for J/Ψ state and the mixed hybrid theory [2] for Ψ (2S) the state.

In section 2 heavy quark hybrid states and mixed heavy quark hybrid states are reviewed. The charm quark c is needed with a mass [3] $m_c\simeq$ 1.27 GeV.

Also, the anti-quark $\overline{c}$ is needed. As discussed in section 2 the state J/Ψ (1S) is $\mathrm{<mo>|</mo>}c\overline{c}\mathrm{<mo\; stretchy="false">(</mo>1}S\mathrm{<mo\; stretchy="false">)</mo><mo>></mo>}$ while state Ψ (2S) is a mixed hybrid c meson.

In section 3, Ψ production in p-p collisions is reviewed. My new work on heavy quark state production is based on the methods used in heavy quark state production in Cu-Cu and Au-Au collisions at $\sqrt{s_{pp}}$ = 200 GeV[4] which used the color octet model [5-7]. Prior to the article [?] Ψ (2S) and Ψ(3S) suppression in p-Pb collisions with E = $\sqrt{s_{pp}}$ = 5.02 TeV was estimated [8] and reviewed [9]. Also, the ALICE collaboration studied J/Ψ production via Xe-Xe collisions at $\sqrt{s_{NN}}$ = 5.44 TeV [10].

Normal and mixed Charmonium States

The starting point of the method of QCD sum rules [11] is the correlator

${\Pi }^A\mathrm{<mo\; stretchy="false">(</mo>}x\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\langle \mathrm{<mo>|</mo>}T\mathrm{<mo\; stretchy="false">[</mo>}{J}_A\mathrm{<mo\; stretchy="false">(</mo>}x\mathrm{<mo\; stretchy="false">)</mo>}{J}_A\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo><mo\; stretchy="false">]</mo><mo>|</mo>}\rangle \mathrm{,}\text{ (1)}$

With |〉 the vacuum state and the current J_A (x) creates the states with quantum numbers A.

With c, $\overline{c}$ and g a charm quark, an anti-charm quark, and a gluon.

For the normal charmonium state J/Ψ (1S)

$J_{c\overline{c}}\mathrm{<mo>=</mo>}{J}_{c\overline{c}}\mathrm{,}\text{ (2)}$

while the mixed hybrid charmonium state Ψ (2S) Jc is

$J_{c\overline{c}g}\simeq -f{J}_{c\overline{c}}+\sqrt{1-f^2}{J}_{c\overline{c}g}\mathrm{,}\text{ (3)}$

where f = 2.

Note that $J_{c\overline{c}}$ creates a normal charmonium state J/Ψ (1S) and $J_{c\overline{c}g}$ creates a hybrid state Ψ (2S).

Differential rapidity cross sections for J/Ψ (1S) Production at E= 510 GeV

In the present work I use the theory described in detail in Ref [12] with applications to BNL-RHIC, LHC and Fermilab, based on the octet model [5-7] for pp production of heavy quark states; and used for studies of pp collisions for Upsilon production at forward rapidities [13] and for heavy quark production at 7 TeV [14] and 8 TeV [15]. This calculation is motivated by the report of preliminary data for J/Ψ, Ψ (2S) production via pp collisions at 510 GeV by the PHENIX Collaboration [16].

For helicity λ =0, the differential rapidity cross section is given by [12]

$\frac{d{\sigma }_{pp\to \Phi \mathrm{<mo\; stretchy="false">(</mo>}\lambda \mathrm{<mo>=</mo>0<mo\; stretchy="false">)</mo>}}}{dy}\mathrm{<mo>=</mo>}{A}_{\Phi }\frac{1}{x\mathrm{<mo\; stretchy="false">(</mo>}y\mathrm{<mo\; stretchy="false">)</mo>}}{f}_g\mathrm{<mo\; stretchy="false">(</mo>}x\mathrm{<mo\; stretchy="false">(</mo>}y\mathrm{<mo\; stretchy="false">)</mo>,2}m\mathrm{<mo\; stretchy="false">)</mo>}{f}_g\mathrm{<mo\; stretchy="false">(</mo>}a\mathrm{<mo>/</mo>}x\mathrm{<mo\; stretchy="false">(</mo>}y\mathrm{<mo\; stretchy="false">)</mo>,2}m\mathrm{<mo\; stretchy="false">)</mo>}\frac{dx}{dy}\mathrm{,}\text{ (4)}$

with with a = 4m²/s=3.46×10^-5, s =E², E = 510 GeV, m = 1.5 GeV (for charm quark) and [12] $A_{\Phi }\mathrm{<mo>=</mo>}\frac{5{\pi }^3{\alpha }_s^2}{288m^{3}s}\mathrm{<mo><</mo>}{O}_8^{\Phi }{\mathrm{<mo\; stretchy="false">(</mo>}}^1{S}_0\mathrm{<mo\; stretchy="false">)</mo><mo>></mo>}=3.1\times {10}^{-4}$ = nb. X(y) and $\frac{dx}{dy}$ are given by (there was a typo in the numerator of $\frac{dx\mathrm{<mo\; stretchy="false">(</mo>}y\mathrm{<mo\; stretchy="false">)</mo>}}{dy}$ , within Ref [12])

$x\mathrm{<mo\; stretchy="false">(</mo>}y\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>0.5}\left[\frac{m}{510}\mathrm{<mo\; stretchy="false">(</mo>}\exp y-\exp \mathrm{<mo\; stretchy="false">(</mo>}-y\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}+\sqrt{{\mathrm{<mo\; stretchy="false">(</mo>}\frac{m}{510}\mathrm{<mo\; stretchy="false">(</mo>}\exp y-\exp \mathrm{<mo\; stretchy="false">(</mo>}-y\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}}^2+4a}\right]$

$\frac{dx\mathrm{<mo\; stretchy="false">(</mo>}y\mathrm{<mo\; stretchy="false">)</mo>}}{dy}\mathrm{<mo>=</mo>}\frac{m}{1020}\mathrm{<mo\; stretchy="false">(</mo>}\exp y+\exp \mathrm{<mo\; stretchy="false">(</mo>}-y\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}\left[1.+\frac{\frac{m}{510}\mathrm{<mo\; stretchy="false">(</mo>}\exp y-\exp \mathrm{<mo\; stretchy="false">(</mo>}-y\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}}{\sqrt{{\mathrm{<mo\; stretchy="false">(</mo>}\frac{m}{510}\mathrm{<mo\; stretchy="false">(</mo>}\exp y-\exp \mathrm{<mo\; stretchy="false">(</mo>}-y\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}}^2+4a}}\right]\mathrm{.}\text{ (5)}$

The gluonic distribution function f_g (x), for $\sqrt{s}$ =E=510 GeV [12], is

$f_g\mathrm{<mo\; stretchy="false">(</mo>}x\mathrm{<mo\; stretchy="false">)</mo>}\simeq 1334.21-67056.5x+887962.0x^2\mathrm{.}\text{ (6)}$

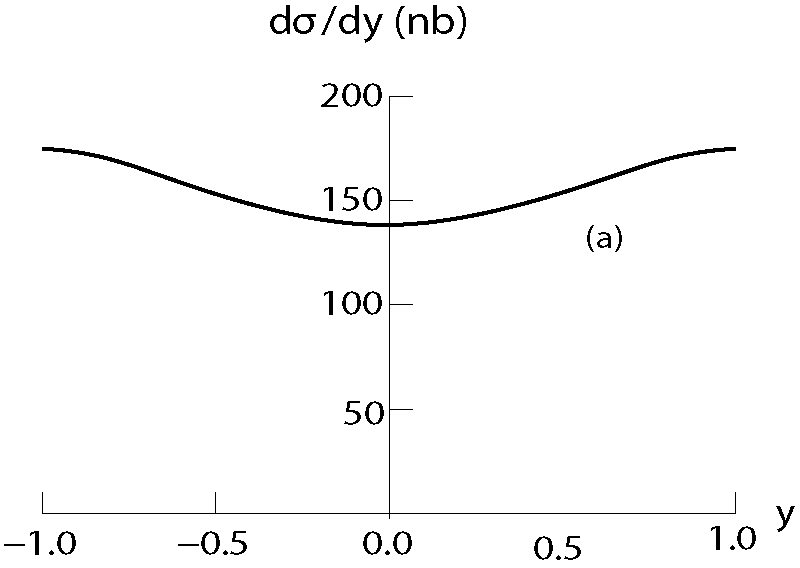
From Eqs(4,2,6) the differential rapidity cross sections for J/Ψ (1S) production via 510 GeV p-p collisions with the standard theory [3] are shown in the figure below.

Figure 1: dσ/dy for E=510 GeV p-p collisions with λ = 0 producing (a) J/Ψ (1S) with a standard C $\overline{c}$ model.

Conclusion

I have calculated the differential cross sections for pp collisions at 510 GeV for J/Ψ (1S) production with the standard $\mathrm{<mo>|</mo>}c\overline{c}\mathrm{<mo\; stretchy="false">(</mo>1}S\mathrm{<mo\; stretchy="false">)</mo><mo>></mo>}$ model. As shown in the figure, $\frac{d{\sigma }_{pp\to J\mathrm{<mo>/</mo>}\Psi \mathrm{<mo\; stretchy="false">(</mo>1}S\mathrm{<mo\; stretchy="false">)</mo>}}}{dy}\simeq$ 150 nb.

The cross-section for J/Ψ (1S) production in the standard model has been found in pp collision experiments at 200GeV [12].

1. Kisslinger LS, Das D. Heavy quark state production in Pb-Pb collisions at = 5.02TeV. JHEP; 2017; 09: 105 (2017)
2. Kisslinger LS. Mixed heavy quark hybrid mesons, decay puzzles, and RHIC. Phys Rev. D. 2009; 79; 114026.
3. Particle Physics Booklet. 2020.
4. Kisslinger LS, Liu MX, McGaughey P. Heavy-quark-state production A-A collisions at = 200 GeV. Phys Rev C 2014; 89: 024914.
5. Cho PL, Leibovich AK. Color-octet quarkonia production. Phys Rev D. 1996; 53: 150.
6. Braaten E, Chen YQ. Helicity decomposition for inclusive production. Phys Rev D. 1996; 54: 3216.
7. Braaten E, Fleming S. Color-Octet Fragmentation and the ψ′ Surplus at the Fermilab Tevatron. Phys Rev Lett. 1995; 74: 3327.
8. Kisslinger LS. Ψ(2S), Υ(3S) Suppression in p-Pb, Pb-Pb Collisions and Mixed Hybrid Theory. Int J Theor Phys. 2016; 55: 1847-1853.
9. Kisslinger LS, Das D. Int J Mod Phys A. 2016; 13: 1630010.
10. Acharya S. Inclusive J/ψ production in Xe–Xe collisions at = 5.44TeV. Phys Lett B. 2018; 785: 419.
11. Shifman MA, Vainstein AI, Zakharov VI. QCD and resonance physics. theoretical foundations. Nucl Phys. B. 1979;147: 385.
12. Kisslinger LS, Liu MX, McGaughey P. Heavy-quark-state production in p−p collisions. Phys Rev D. 2011; 84: 114020.
13. Kisslinger LS, Das D. Upsilon production in pp collisions for Forward Rapidities at LHC. Mod Phys Lett A. 2013; 28: 1350067.
14. Kisslinger LS, Das D. Ψ and Υ Production In pp Collisions at 7.0 TeV. Mod Phys Lett A. 2013; 28: 1350120.
15. Kisslinger LS, Das D. Mod Phys Lett A. 2014; 29: 1450082.
16. Durham JM. PHENIX Collaboration. Science Direct. Nuc Phys A. 2014; 1.
17. Kisslinger LS. Mixed Heavy Quark Hybrid Mesons, Decay Puzzles, and RHIC. Phys Rev. 2009, 79: 114026.