Introduction
The resolution of physical phenomena formulated by partial differential equations using the finite element method requires a regular mesh (in the isotropic case) specifically for the convergence of the method. General discussions about mesh quality measures can be found in [1.2]. To quantify this regularity several shape quality measures have been introduced in [3,4] using various approaches and compared in [5-12] for simplexes in 2D and 3D. Many of them are implemented in the Verdict library [13].
Among all the possible definitions let us notice the radius ratio (or sometimes called aspect ratio) [14]:
Where d is the dimension of space and rin, rout, are respectively the inradius and the circumradius of the simplex. Another well-known quality metric is the mean ratio n [5] (explicitly used in [15]) which was already used in [16] and redefined in [17]:
Those two measures are compared in [18] and used for instance in [19].
In [9] the author define a new method to unify various mesh quality metrics using an algebraic approach.
In this paper, we introduce the covariance edges matrix which allows us to characterise the regularity of the mesh elements (polygons and polyhedrons). By analysing the eigenvalues of this matrix we define several shape quality measures for convex elements.
Covariance edges matrix
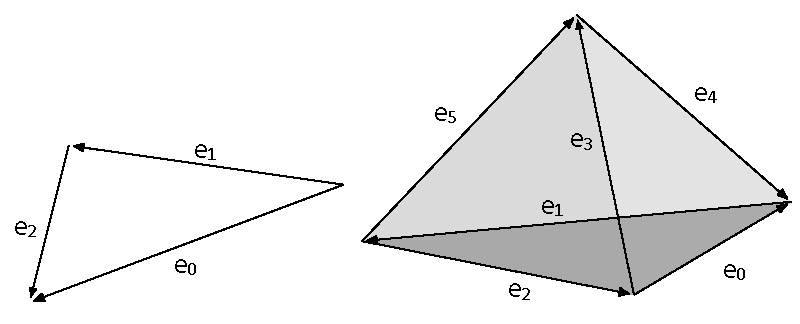
Let p be a polygon or a polyhedron in Rd (d = 2 or d = 3) with n edges and let denote its edge column vector by
as in Figure 1. For our application, we can set ei = vj - vj or ei = vj′ - vj with vj and vj′ the two vertices of the edge ei.
Figure 1: Notations for 2D polygon and 3D polyhedron.
Following [17,20], the covariance edges matrix N associated to P is defined as:
Each eieiT is a symmetric rank-1 covariance matrix associated with an edge i of P. For a polyhedron in 3D, these matrices are:
As stated previously, we notice that each eieiT and N does not depend on the direction (order of starting and ending point) of the vector ei.
For regular polygons (Lemma 7) or some polyhedrons (tetrahedrons in Lemma 14, cubes in Lemma 15, prisms in Lemma 16, and octahedrons in Lemma 18) we will show the regularity lemma:
Where h is the length of all edges, X is the dimension of the space (2 or 3), and ld is the identity matrix in Rd. Besides, we will show (Lemma 17) that for a regular pyramid, this matrix is only diagonal on some basis (and not proportional to the identity). However, the regularity of the pyramid can be obtained by completing the pyramid to obtain an octahedron (see Lemma 19).
Hence, for a regular polygon or specific polyhedron, the covariance matrix has one eigenvalue of multiplicity d. Based on the invariants of the covariance edges matrix we can thus define several measures to quantify the gap between the eigenvalues for a general polygon or a polyhedron in order to obtain the corresponding shape quality measure.
At first, we developed some properties of N. These properties are used to prove the above regularity lemma. Then, we proposed shape quality measures.
Properties of the covariance edges matrix
In this section, some properties of the covariance edges matrix are given, namely the positive definiteness, the geometric invariants, and the commutativity with orthogonal matrices which keeps the polygon or polyhedron invariant. These properties will then be used to prove the regularity lemma in 2D and 3D.
Before the lemmas, we start with a remark that will be useful for the prisms and pyramids.
Remark 1: A matrix proportional to the identity matrix (ld) is invariant by a change of basis. This is not the case for a general diagonal matrix such as:
General properties
Lemma 1: N is a symmetric positive-definite matrix.
Proof. N is symmetric by construction. Let X be a non-zero vector, we have:
And XTNX = 0 implies that X must be orthogonal to all ei which is only possible with X = 0, so XTNX > 0.
Lemma 2 (Commutativity with special orthogonal matrices): Let Q be an orthogonal matrix that defines a bijective mapping between the edges. That is to say such that Qei = eσ(i) with a permutation.
Q commutes with N.
Proof.
Which leads to QN = NQ as Q-1 = QT because Q is an orthogonal matrix.
Example 1: An example of such Q for a regular polygon in 2D is the rotation matrix of angle
where n is the number of edges. Using, this rotation leads to Qei = ei+1 for 0 ≤ i < n with en := e0.
Link with the metric of simplex: In the case of a simplex (triangle in 2D and tetrahedra in 3D), one may find a link between the covariance edge matrix N and the metric of the element M. This matrix is such that eiTMei = 1. Besides in [17,20], they show that:
Properties in 2D: From Lemma 1, N is symmetric. In this section, we will denote N as:
First, the computations of the two invariants (trace and determinant) are made, then we use the commutativity from Lemma 2 to prove the regularity of Lemma 7 already stated in (3).
Invariants in 2D: For d = 2, the two invariants (trace and determinant) of the covariance edges matrix N are linked to the squared edge length and the squared area of all parallelograms made up of two different edges as stated in Lemmas 3 and 4.
Lemma 3 (Invariants in 2D: trace): For d = 2, the trace of the covariance edges matrix N is:
Proof.
Lemma 4 (Invariants in 2D: determinant): For d = 2, the determinant of the covariance edges matrix N is:
Proof.
Remark 2: The sum (7) is composed of the area of all parallelograms made with two different edges. In the case of a triangle, this sum may be simplified to:
with |T| the area of the triangle T.
Invariances by isometric transformations in 2D: In Lemmas 5 and 6, we show the form of the covariance edges matrix when the polygon is invariant by reflection or rotation.
Lemma 5 (Effects of 2D reflections): Consider a polygon P in 2D. If this polygon is invariant by a reflection then the covariance edges matrix is diagonal.
Proof. In 2D the two main reflections are:
From Lemma 2, we know that QXN = NQX, it leads to:
The same computations can be done with QY and we have in both cases:
Lemma 6 (Effects of 2D rotations): Consider a polygon P in 2D. If this polygon is invariant by a rotation of angle θ (different of 0[]) then the covariance edges matrix is proportional to the identity:
Proof. Let Q be the rotation matrix of angle θ which let invariant P:
With S ≠ 0 as the angle is different of 0[π]. The case θ = 0[π] is not meaningful, as Q = ± l2.
From Lemma 2, we know that QN =NQ. Using the notations from (5), we have:
So
.
Applications in 2D
Lemma 7 (Applications to regular polygons in 2D): For a regular n-gon in 2D with an edge length of h, the generic formula (3) holds and the covariance edge matrix is equal to:
Proof. Using Lemma 6 with a rotation of angle
we get N = al2. Besides, from (6) of Lemma 3, we have a regular polygon tr(N) = nh2. Moreover, we know that tr(N) = 2a. We can conclude that
.
Remark 3: Using the polar coordinates of the vertices a proof of Lemma 6 and 7 can be made using direct computations.
Properties in 3D: We are now working with polyhedrons in three dimensions (d = 3). With Lemma 1, N is symmetric and we will denote N as:
Invariants in 3D: When using a matrix of size three, we have three invariants: determinant, trace, and α1 the coefficient of degree one in the characteristic polynomial of the matrix:
In Lemmas 8, 9, and 10 we compute these invariants.
Lemma 8 (Invariants in 3D: trace): As in 2D in Lemma 3 the trace gives the sum of the squared length of all edges:
Proof.
Lemma 9 (Invariants in 3D: $_1$): Proof. Computations give the following formula for the invariant α1:
Remark 4: For a tetrahedron, computations done in Chapter One of [17] give:
Where | Tf | is the area triangle face f.
Lemma 10 (Invariants in 3D: determinant): Proof. The determinant is:
Remark 5: Following the computations from [17,20] we have for a tetrahedron:
Where |T| is the volume of the tetrahedron.
Remark 6: It is more complex to extract geometric expressions of det(N) and 1 for other regular polyhedrons.
Invariances by isometric transformations in 3D: In the following lemmas, we show the form of the covariance edges matrix when the polyhedron is invariant by various isometric applications.
Lemma 11 (Effects of 3D axis reflections): Consider a polyhedron P in 3D. If this polyhedron is invariant by two reflections around planes then the covariance edges matrix is diagonal.
Proof. Let Q be the reflection around the plane z = 0:
If the polyhedron is invariant by Q Lemma 2 holds and we have QN = NQ. This leads to:
In the case of the reflection around the plane y = 0 we have:
and for the plane x = 0:
If two of the three reflections let the polyhedron invariants, we can conclude that N is diagonal.
Lemma 12 (Effects of 3D axis rotations) Consider a polyhedron P in 3D. If this polyhedron is invariant by a rotation around one axis with an angle θ (θ ≠ 0[π]) then the covariance edges matrix is diagonal.
Proof. Let Q be the rotation matrix around the z-axis with θ angle:
We avoid the case ∅ ≠ 0[π] in order to remove the case Q = 1 and the case of the reflections done previously in Lemma 11 as Rz(π) = -Qrz.
In this case, if the polyhedron is invariants by Q, Lemma 2 holds and computations similar to the ones done in 2D (Lemma 6) of NQ = QN give:
With Q = Ry(∅)it leads to:
and for Q = Rx(∅)we have:
In all three cases, the covariance edges matrix is diagonal.
Lemma 13: Let P be a regular polyhedron with n edges with the length of h which is invariant by two rotations of angle different of 0[π] with two different axis. The generic formula (3) holds and the covariance edges matrix is equal to:
Proof: Let us build a basis by taking the two rotations axis and a third vector. On this basis, we can apply twice Lemma 12 to get a matrix proportional to the identity N = al3. Then using Lemma 8 and the computations of trace (8) we get tr(N) = 3a = nh2. It leads to .
Besides, as the covariance edges matrix is proportional to the identity it will be the same in all bases as stated in Remark 1.
Applications in 3D
Lemma 14 (Applications to tetrahedrons): For a regular tetrahedron with an edge length of h, the generic formula (3) holds and the covariance edge matrix is equal to:
Proof: A regular tetrahedron is invariant by rotations of the angle
around the axis from one vertex to the center of the opposite face. Applying Lemma 13 gives the results.
Lemma 15 (Applications to cubes): For a regular cube with an edge length of h, the generic formula (3) holds and the covariance edge matrix is equal to:
Proof: A cube is invariant by three rotations of angle
with an axis going from the center of the current face to the opposite face. Lemma 13 holds and we get N = 4h2l3.
Remark 7: The proof can also be done by considering the cube as a prism with a square basis (see Lemma 16).
Lemma 16 (Applications to prisms): For a regular m-prism with n = 3m edges of size h, the generic formula (3) holds and the covariance edge matrix is equal to:
Proof: Let be a basis with the two first vectors inside the plane of the m-gon. Let be the last vector orthogonal and going from the center of one polygon to the other. Along this last vector, a prism is invariant by a rotation of angle
, so Lemma 12 applies and we get:
Let v be one edge vector collinear to the rotation axis. We have Nv = fv. Besides:
For all ei in the two m-gons we have (ei. v) = 0. For the others, we have (ei. v)ei = h2v as all the vectors are collinear. This leads to Nv = mh2v. From Lemma 8 and the computations of the trace (8), we have that tr(N) = nh2 = 3mh2 and here we have tr(N) = 2a+f. Everything leads to:
We can conclude that
. This result is valid on all basis as stated in Remark 1.
Lemma 17 (Applications to square pyramids): For a regular square pyramid with an edge length of h, the generic formula (3) does not apply as the covariance edges matrix is only diagonal on a specific basis. This basis is defined by taking the two first vectors in the plane of the square. The last vector is orthogonal to the two firsts and goes from the center of the square to the opposite vertex. On this basis, the covariance edges matrix is:
Proof. In a basis where the last vector is going from the center of the square to the opposite vertex, Lemma 12 applies with an angle of
and we get in this basis:
From Lemma 8 and the computations of the trace (8) we get:
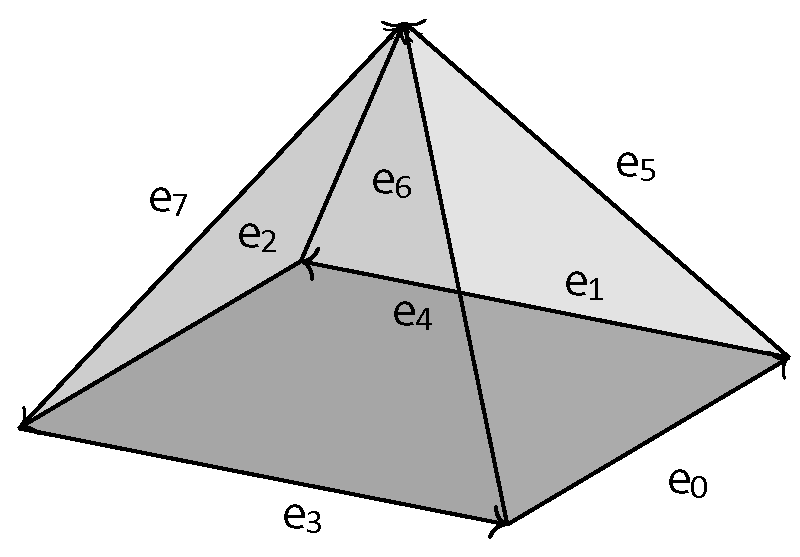
Let e0 be one side of the square as in Figure 2. We have:
Figure 2: Indexes of vectors in a square pyramid.
By recomputing directly this product, we get:
Everything leads to:
e can conclude that for a regular square pyramid on a specific basis, we have:
Remark 8: From Remark 1, we recall the fact that the covariance edges matrix for a pyramid is only diagonal in a basis composed of two vectors in the square, and the third vector is orthogonal to the two firsts and going from the center of the square to the opposite vertex.
Lemma 18 (Applications to octahedrons): For a regular octahedron with an edge length of h, the generic formula (3) holds and the covariance edge matrix is equal to:
Proof. An octahedron is invariant by three rotations of angle
:
- one with the axis from the center of the square to the two vertices not belonging to the square
- two with the axis joining two opposite vertices of the square.
Lemma 13 holds and we get N = 4h2l3.
Lemma 19 (Applications to symmetrized pyramids): As a pyramidal element is not a regular polyhedron, we propose to complete this element by a symmetric part to obtain an octahedron. To this end, the opposite apex is the symmetrical point of the current apex with respect to the centroid of the opposite quadrilateral face. For the obtained octahedron one can apply Lemma 18 to get:
Remark 9: The formula (3) is verified numerically for all five Platonic solids, all thirteen Archimedean solids, and some of the Johnson solids. It is not valid for anti-prisms (as for the square pyramid).
Shape quality using the covariance edges matrix
Shape quality measures: The covariance edges matrix N is proportional to the identity of regular elements which are isotropic. When moving to anisotropic elements, this matrix is no more proportional to the identity. One may use this property to define shape quality measures.
One of the possible shape quality measures of a polygon P is defined as:
Where λmin and λmax are the smallest and greatest eigenvalues of the covariance edges matrix N. This ratio of the eigenvalues defines the anisotropy of the matrix.
If the computations of eigenvalues are too costly, one may use the ratio of the means of the eigenvalues as an alternative, as we can use the invariants of the matrix to define means. In 2D, the computations of the Arithmetic, Geometric, and Harmonic means of λ1 and λ2 give:
Let us recall, that these two eigenvalues are real and positive as the covariance edges matrix is symmetric positive-definite (Lemma 1). The means are then positive. Besides, let us notice that 0 < H ≤ G ≤ A. We can then, define qualities between 0 and 1 by computing the ratio of two means:
One can easily notice that qGA = qHG and that qHA = q2GA. Besides, for a triangle, these new qualities are equivalent to the mean ratio η (1) as we have:
Extension of the quality for degenerated elements
In the case of a degenerated quadrilateral:
the covariance edges matrix is:
Which gives, qλ = qGA = 1 which is not satisfactory as we want to avoid such elements. To overcome this difficulty, we introduce the jacobian of the elements in the quality, for instance:
where α is a parameter to give more or less influence to the Jacobian and Jmin (Jmax) is the minimal (maximal) value of the Jacobian over the elements. In the next sections, we set α = 1/3.
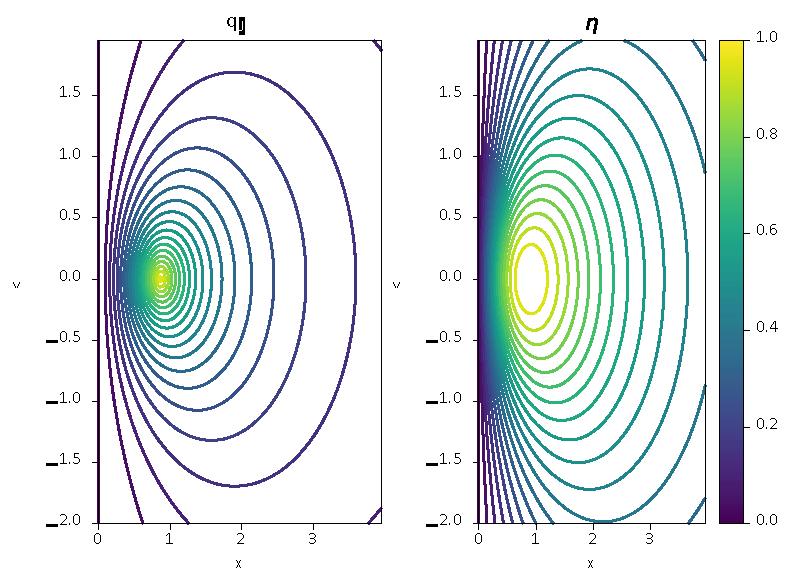
Applications on triangles: In the spirit of [11] we computed in Figure 3 the qualities of triangles ABC defined as:
Figure 3: Comparison of qualities on triangles (left:
qJλ (11), right:
η (1)).
For each point, B(x,y) we compute the quality of the resulting triangle. In the case of triangles, the value of
in (11) is equal to one. The results show a behaviour similar to the mean ratio (1)
Applications on quadrilaterals: Using the same idea for quadrilaterals, we computed in Figures 4,5 the qualities of various quadrilaterals. For the quadrilaterals, the ratio
of (11) is computed using the minimal and maximal values of four determinants [21]:
Figure 4: Comparison of qualities for quadrilaterals with two edges from the unit square (left:
qJλ (11), right: min
i∈[1;4](
η(Ti)) (12)).
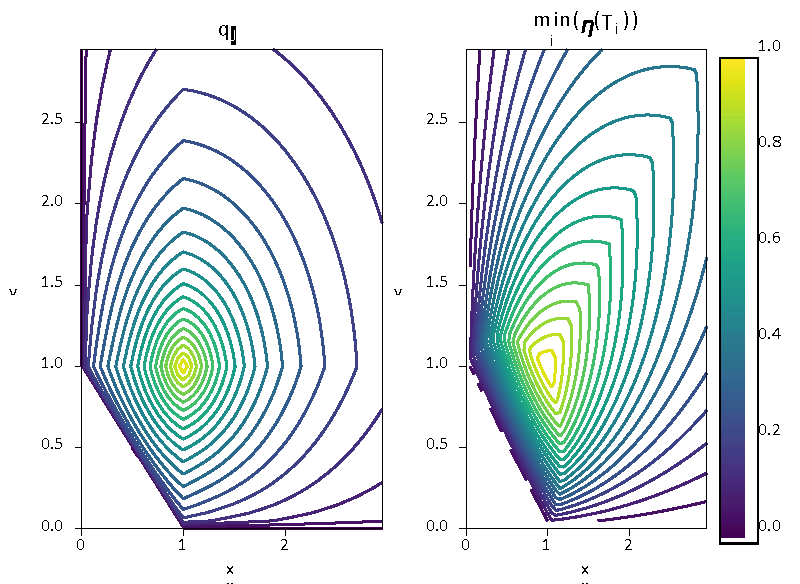
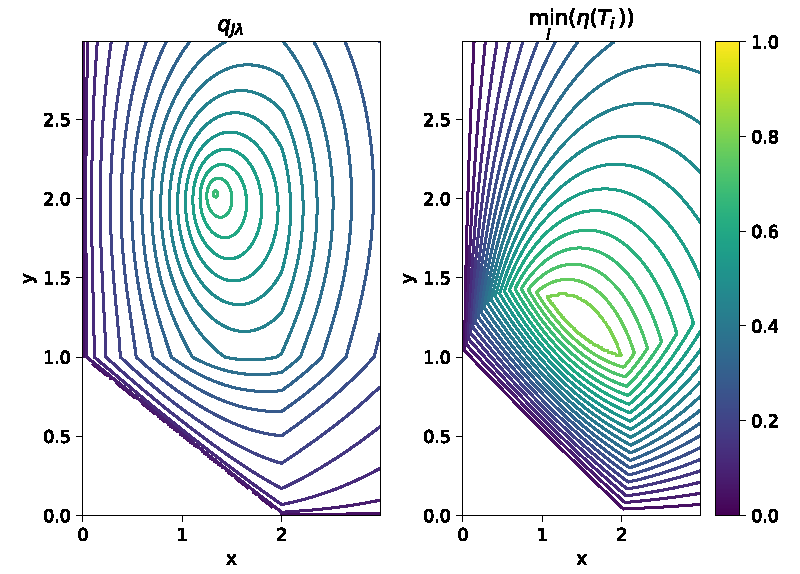
Figure 5: Comparison of qualities for quadrilaterals with two edges from a rectangle (left:
qJλ (11), right: min
i∈[1;4](
η(Ti)) (12)).
The comparison is made between qjλ (11) and the quality defined as:
where the Ti is one of the four possible triangles made in a quadrilateral Q when cutting it into two triangles.
Figure 4 is obtained for several quadrilaterals OABC defined as:
In this case, the element with the greatest quality is the unit square S according to both qualities as qjλ (S) = q(S) = 1.
Figure 5 is obtained for several quadrilaterals OABC defined as:
In this second case, the two qualities differ. In Figure 6, the elements with better quality are presented. qjλ tends to have the best element for (x,y) = (1.35,2.05) with a quality near 0.67 whereas when splitting into two triangles (12) it gives a maximum for (x,y) = (1,2) with a quality of 0.8. The choice of qjλ may be better as the element is more isotropic (the ratio of the minimal length over the maximal length of edges is greater). Besides, only on global maximum is found whereas when splitting into triangles there is a zone where all the quadrilaterals have a quality near 0.8 which is not convenient to do optimisation on shape quality measure.
Conclusion
A new algebraic shape quality measure for polygons and polyhedrons is introduced. This measure depends only on the covariance edges matrix, namely the ratio between the smallest and the greatest corresponding eigenvalues. Using the invariants of this matrix, several alternative shape quality measures are also proposed. In particular, one of the proposed measures, applied to simplicial elements, coincides with a known geometric measure. Hence, this measure can be seen as a generalisation to other elements. The novelty of this measure is its generality: in this work, it is applied only to triangles and quadrilaterals but future developments will focus on 3D applications. The application to mesh optimisation is the next step and the main advantage of this new measure is the fact that it is the same expression for all elements.
As shown in [17] and recalled in Section 3.2, the covariance edges matrix is related to the metric of the element for the simplicial element. It is interesting to investigate the generalisation of the metric element for non-simplicial elements based on the covariance edge matrix.
The extension of the covariance edges matrix to high-order elements may require more investigation, in particular, the element edges are curved, and differential geometric must be taken into account.
 This work is licensed under a Creative Commons Attribution 4.0 International License.
This work is licensed under a Creative Commons Attribution 4.0 International License.
 Help ?
Help ?



 Save to Mendeley
Save to Mendeley