Open path theory: Pattern and structure in prime numbers

The Open Path theory, supported by experimental data, is presented. The main hypothesis proposes that Prime Numbers's positions are determined by previous Prime Numbers as well as their spacing, in a complex, but deterministic way. The concepts of Open Path, Perfect Space, and Primorial Perfect Space are introduced. The Open Path theory can predict prime gaps of any minimum predetermined size. Two rudimentary algorithms based on this theory are presented. The first algorithm returns a sample (a few hundredth of numbers) containing 25 % of Prime Numbers at distances above 1011. The mirrored sample gives a similar percentage of Prime Numbers. The algorithm execution time is of a few milliseconds. The second algorithm presented determines if a number belonging to a Perfect Space is a composite number or a Prime Number.

Introduction

The distribution of prime numbers within the realm of natural numbers has historically been perceived as highly enigmatic and seemingly devoid of any discernible order [1] or predictability [2]. These early viewpoints characterized prime numbers as if they were scattered at random throughout the number line [3], defying any attempts to pinpoint a systematic pattern.

However, more recent research has provided a nuanced perspective on the distribution of prime numbers. Notably, the work of mathematicians like Tao (referenced as [4]) has unveiled the presence of numerous hidden patterns within the prime number distribution. Contrary to the earlier belief that primes were purely random, these studies have demonstrated that the distribution of prime numbers is not chaotic but rather can be described by mathematical equations, as illustrated by Ferreira's research [5,6].

In essence, the evolving understanding of prime number distribution suggests that while it may appear disorderly at first glance, it is not truly random. Instead, it adheres to underlying mathematical principles and can be expressed and characterized by equations, shedding light on the fascinating structure that lies beneath this seemingly chaotic mathematical landscape.

The present work continues the former research path, sketching up a theory about the pattern and structure in the Prime Number distribution based on OP. An OP conceptualizes the path that follows the distribution of Prime Numbers, defining a series or path where the probability of finding a Prime Number is very high. By opposition, a CP refers to a series or path where the possibility of finding a Prime Number is null. The theory is presented in the form of a thought exercise, including the effect of spacing, or Prime Number gap, in the pattern of Prime Numbers. The PS and PPS concepts are also introduced. A PS (or a PPS) determines the pattern in the distribution of Prime Numbers. The pattern defined is found in the consecutive replicas of the PS. Section 2 is dedicated to presenting the OP Theory and explaining the main concepts related to it. At the end of the Section, there has been made some predictions regarding the gaps between Prime Numbers. Section 3 presents an experimental analysis of the distribution of Prime Numbers to show evidence of the underlying and complex pattern present in the Prime Number distribution. A simple algorithm based on this theory is proposed. Another very simple algorithm based on OP is also presented to determine if a number in a PS is a composite of two numbers. If it is composite, the algorithm returns the two divisor numbers. The results are discussed in Section 4, and finally, some conclusions are presented in Section 5.

The open path theory

One

In the beginning, God created the heaven and the earth¹, and the One appeared. One. To generate the complete space of positive natural numbers, One replicates himself², with a spacing of One. (1, 2, 3, 4, 5, 6, .....) From now on, the series will be annotated in two different ways, both of them equivalent. The first one is annotated in the form of a series. Equation 1 represents the first OP for Prime Numbers, as following this path it is possible to find Prime Numbers³.

-------------------------------

¹Genesis 1:1, King James Version

²Isidoro de Sevilla, as expressed in de Mathematica, already believed, back in the VI century, that One was the seed of all the rest of numbers, but not a number.

³In this case, any, since it is the first OP. Each OP represents a new constrain to the position of Prime Numbers, as they cannot be in CP

$1\cdot n+\mathrm{1<mo>=</mo>1,2,3,4,...}\text{ (1)}$

And the second one is annotated in the form of spacing, where the spacing (the superscript) between the different elements inside a PPS is described (Equation 2). The subscript shows the Prime Number to which applies the series. This notation will help to see graphically the patterns inside the PPS. The pattern described by the sequence of spacing replicates infinitely, being equivalent to the series notation.

$1One\mathrm{<mo>\{</mo>}+\mathrm{1<mo>\}</mo><mo>=</mo>1,2,3,4,...}\text{ (2)}$

The pattern defined by One can be seen in the first numbers up to 22. The only component of One-PPS is One. One-PPS defines a unique OP, the one defined by Equations 1 and 2. There is no CP.

Perfect space and primorial perfect space: A PS determines the pattern in a region of positive natural numbers differentiating between composites of the Prime Numbers that define the PS (not members of the PS) and those composites of other Prime Numbers or Prime Numbers (members of the PS). The members of the PS define the phase or start of the OP. The length of the PS and the multiplicative factor of the OP are determined by the multiplication of all the Prime Numbers defining the PS. The first element of a PS is always One. The PS has a symmetrical structure⁴ and the pattern defined presents infinite consecutive replicas of the PS. If the Prime Numbers are consecutive and start in One, then, the PS is called PPS. The length of the PPS and the multiplicative factor of the OP defined by it are the primorials.

---------------------------------

⁴with the exception of 2-PPS, that is not symmetrical

Two

With the space of positive natural numbers already generated, it is possible to find the number closer to One, and separated from him exactly one space, the number two. The 2-PPS is formed by the union of two One-PPS:

$1One\mathrm{<mo>\{</mo>}+1+\mathrm{1<mo>\}</mo>}\text{ (3)}$

Then, two are removed, completing the process and creating a new PPS:

$\mathrm{12<mo>\{</mo>}+\mathrm{2<mo>\}</mo><mo>=</mo>1,3,5,7,...}\text{ (4)}$

The same process is done with the aid of series, defining the transformation that will be repeatably used from now on. The even series is defined by Equation 5:

$2\cdot n+2\text{ (5)}$

This series is subtracted from the series of One, Equation 1. The last series is segmented into two different series, one with the even numbers and another one with the odd numbers:

$1\cdot n+\mathrm{1<mo>=</mo>}\{\begin{array}{lll}\hfill & \hfill & 2\cdot n+1\hfill \\ \hfill & \hfill & 2\cdot n+2\hfill \end{array}\text{ (6)}$

The final result of the subtraction is, naturally:

$1\cdot n+1-2\cdot n+\mathrm{2<mo>=</mo>2}\cdot n+1\text{ (7)}$

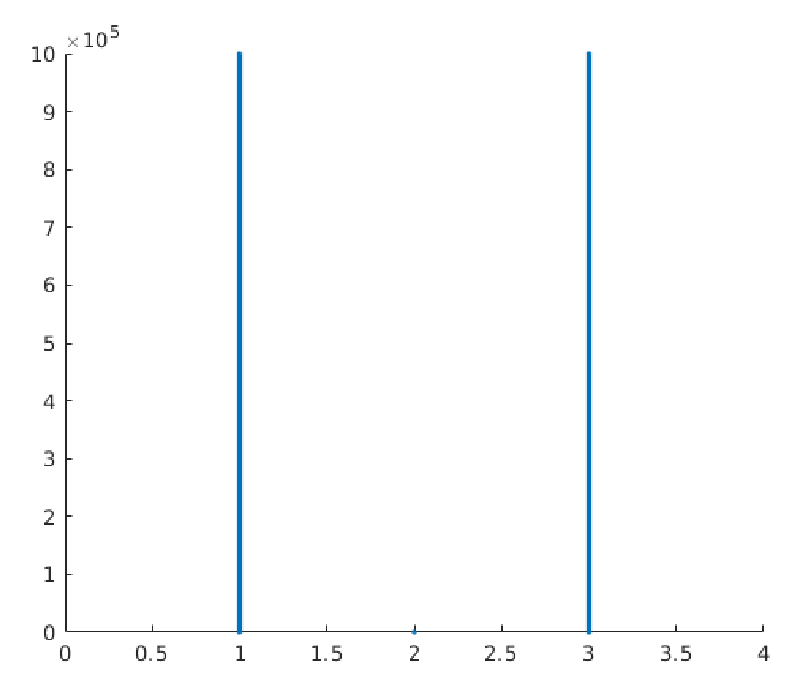
Resulting in a series of odd numbers. This defines the outcome series of 2-PPS. The odd series is an OP, while the even series is a CP. The pattern defined by 2-PPS is seen in the Prime Number series up to 32, and it is underlying in future PPS. Although it is also evident, this pattern is shown in Figure 1. The pattern created by the 2-PPS is defined by the distribution of the natural numbers that have a spacing of +2 between them^5,6.

----------------------------

⁵The odd series goes to One, while the even series goes to Zero. CP are series that start or go to Zero, while OP are series that either go to One, or to another Prime Number, what would make the Prime Number proxies of One

⁶The generation of the even series can be explained as the simple removal of two, as it creates a perturbation bringing the space of number out of equilibrium, the removal of four follows and so on, trying to balance the full set of natural numbers. The PPS can be explained as a region where their components (Prime Numbers and Perfect Composites) find the most stable positions. Once this equilibrium is lost, by the effect on the next Prime Number, a new PPS is generated where equilibrium is found, although again, ephemerally.

Three

Let's continue our numeric excursion. The following Prime Number is three. It is the first number, after One, in the 2-PPS OP. Its appearance modifies the previous PPS, generating a new one. The length of the 3-PPS increases to six, the primorial of three, and where the series of three finds the series of two (and the one of One). The members of the pre-3-PPS are (1,3,5). If the spacing notation is used, the transformation to be performed implies the combination together of three of the previous 2-PPS⁷:

----------------------------

⁷It represents the jump from One to the following element of the PPS, but it would be more appropriately defined if it starts in zero. For a better visualization it is left like this

$\mathrm{12<mo>\{</mo>}+2+2+\mathrm{2<mo>\}</mo>}\text{ (8)}$

The removal of three results in a spacing defined as:

$\mathrm{13<mo>\{</mo>}+4+\mathrm{2<mo>\}</mo>}\text{ (9)}$

The same process is performed with series. First, the 2-PPS series is segmented to the size of the new PPS:⁸

-------------------------

⁸At this step, if the CP is followed, we will be lost in the infinite space of numbers. Exactly as it would happens if Prime Numbers are searched in even numbers, following the CP, instead the OP (2 n+1)

$2\cdot n+\mathrm{1<mo>=</mo>}\{\begin{array}{lll}\hfill & \hfill & 6\cdot n+1\hfill \\ \hfill & \hfill & 6\cdot n+3\hfill \\ \hfill & \hfill & 6\cdot n+5\hfill \end{array}\text{ (10)}$

The series that has to be removed is the one with phase three. The final result will be the remaining two series:

$\mathrm{<mo\; stretchy="false">(</mo>2}\cdot n+\mathrm{1<mo\; stretchy="false">)</mo>}-\mathrm{<mo\; stretchy="false">(</mo>6}\cdot n+\mathrm{3<mo\; stretchy="false">)</mo><mo>=</mo>}\{\begin{array}{lll}\hfill & \hfill & 6\cdot n+1\hfill \\ \hfill & \hfill & 6\cdot n+5\hfill \end{array}\text{ (11)}$

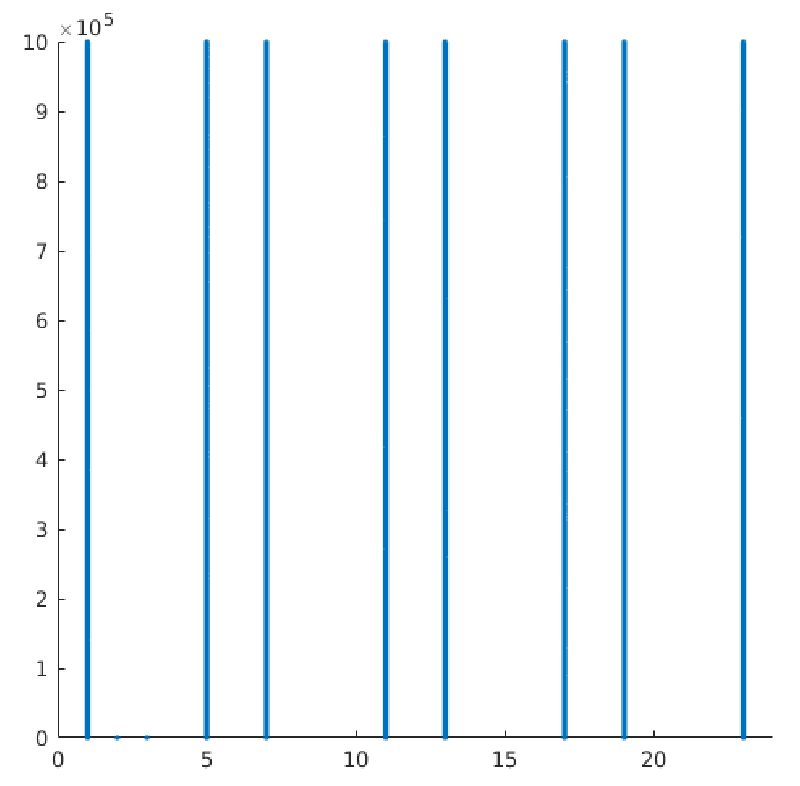
The 3-PPS is defined by One and 5. The length of the 3-PPS is six, the primorial of three. And it is completely symmetric: The distance from zero to One is the same as from six to five. The pattern generated by the 3-PPS, defined by Equation 9, can be seen completely up to 52 (1, 5,7,11,13,17,19,23). It also underlies the rest of the Prime Number series as it is shown in Figure 2.

The close path: The series to remove from a pre-PPS, generated by the addition of a number of previous PPS equal to the Prime Number being evaluated, are those with a phase equal to the Prime Number multiplied by the pre-PPS members. In the case of 3-PPS, the components of the pre-PPS are 1,3 and 5. The result from multiplying them by the Prime Number, three, gives the values of 3, 9, and 15. As only 3 are inside the limits of the 3-PPS, then this will be the only member that will be removed from the list of OP.

The open path: The remaining series are OP, to One, either directly -it will be seen later that the +One path⁹ is always open- or by any of their proxies, an active Prime Number member of the PPS or a Perfect Composite inside the limits of the PPS. A Perfect Composite is a Composite lower than the primorial and not divisible by the Prime Numbers lower than the one defining the PPS. A Perfect Composite acts as an OP. The Non-Prime Numbers generating OP should be of a higher order than the PPS, that is, not divisible by the Prime Number defining the PPS or other smaller Prime Numbers.

-------------------------

⁹It can called the Primordial Path

Spacing between prime number: If the OP defines a series where Prime Number can be present, the CP excludes the presence of Prime Number. This property can be used to determine regions of the space where there will not be Prime Numbers. In a PPS, the spaces are CP. And the spacing between One, which is always an OP, and the next OP, which is usually the first Prime Number after the one defining the PPS, is replicated with a distance equal to the PPS length. For instance, in the 7-PPS, there is a spacing between One and 11. The primordial of seven, the length of the 7-PPS, is 210. So there will be a space without Prime Numbers in the region defined by 210 . n+(2 ...10). So the regions between 212 and 220, 420 and 430, 630 and 640, etc will not contain Prime Numbers. The higher the order of the PPS, the higher the first spacing. Also, it will be present deep in the space as the replicas are determined by the primorial. The 1009-PPS will define a spacing of 1012, and the first occurrence of this spacing will take place in his primorial+One. So after 19766653710804075182143870771990238475539088142104672537897548776929384313227289497808619213628587662490595625147474943321532235492742204128846913537770322864572995974935654100594289056885746177674106727111011492167293600757722582873710083333409221248630824126186603003458015947013676475012954103807759699698139884769988141115940629691053820740641161140263635520790129447288872867072881843138566340347306438762146043190 + One, there will be a spacing of more than 1000 numbers, a region without Prime Numbers. At each replica of the 1009-PPS, the space without Prime Numbers will appear again. Never look for Prime Numbers in the even series and never look for Prime Numbers in the first 1012 numbers after the multiples of the 1009 primorial + One. The PPS defines also the positions where there cannot be Prime Numbers. The replicas of the PPS will not have Prime Numbers in the spacing of the PPS and will have the possibility to have Prime Numbers only in the positions of the PPS members. The phases of the OP are the Prime Number and Perfect Composite Numbers in the PPS. As the PPS is symmetric, the same applies to the symmetrical part. The regions between 210 . n- (2 ...10) will also not contain prime numbers.

Open path primality hypothesis: A Prime Number will always be allocated in an OP. The condition is necessary but not sufficient.

Final considerations of three: Three considerations about the 3-PPS. The first one is completely symmetric, a symmetry that will be inherited by consecutive PPS and that will be maintained through PPS with more complex and complicated patterns. The symmetry can be observed when the series 6 . n+1 is brought backward to the negative space of numbers:

... 13, 7,1, -5, -11 ...

Secondly, it shows another general rule: each pattern generated by a PPS is symmetric (as it has been said before) and it is enchained with consecutive replicas of the PPS by a spacing of two. The third characteristic to note is that the spacing from the first element of the PPS (and its replicas) is equal to the distance from One to the consecutive Prime Number that generates the PPS. In the case of three, the distance is four, as can be observed in Figure 2.

Five

To create the 5-PPS, the spacing notation will be used first. Five¹⁰ of the 3-PPS are linked together:

--------------------------------

¹⁰Note that the last spacing (+2) is the linking one, it is outside the symmetric part. Also note that the proper notation would imply +1 at beginning and +1 at the end. But the notation used allows an easy visual detection of the pattern.

$1_3\mathrm{<mo>\{</mo>}+4+2+4+2+4+2+4+2+4+\mathrm{2<mo>\}</mo>}\text{ (12)}$

Resulting in a pre-PPS with a length of 30, the primorial of five. Removing the number five (5 × 1) and number 25 (5 × 5)¹¹ results in the pattern defined by Equation 13:

------------------------------

¹¹Remember that the numbers to remove from the pre-PPS are the ones that result from multiply members of the previous PPS by the Prime Number being evaluated.

$1_5\mathrm{<mo>\{</mo>}+6+4+2+4+2+4+6+\mathrm{2<mo>\}</mo>}\text{ (13)}$

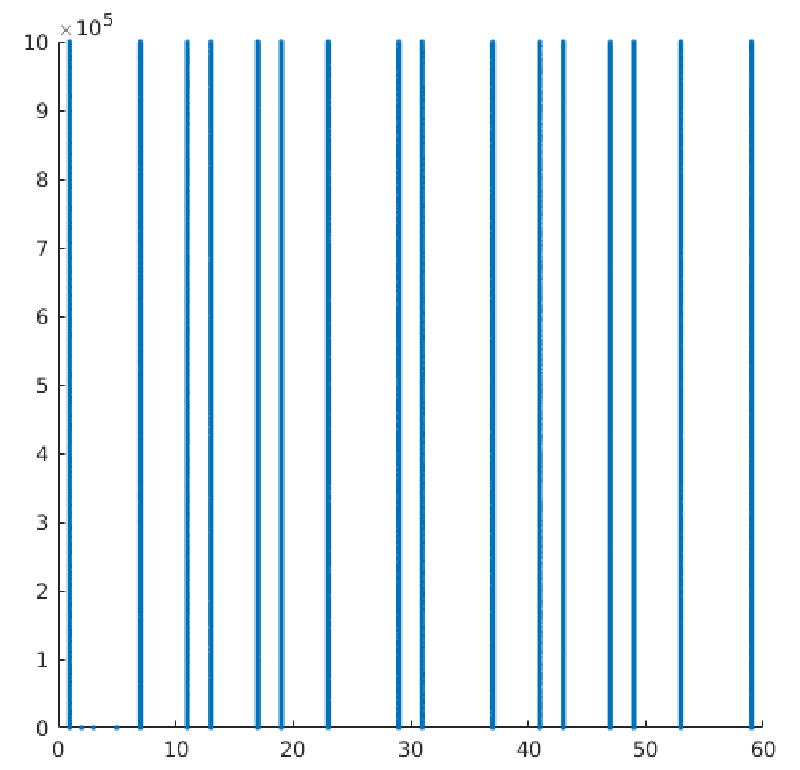
The pattern of 5-PPS can be seen clearly up to 72 (1 7 11 13 17 19 23 29 31 37 41 43 47). The pattern created by the 5-PPS can be seen in Figure 3.

To create the 5-PPS, only one of the two OP from the 3-PPS will be used, as the other part of the 5-PPS can be obtained by primorial symmetry. The primorial OP of the 3-PPS (Equation 14) is unfolded up to 30, obtaining the list of possible candidates for the 5-PPS. The sequence obtained is 1, 7, 13, 19, and 25 being the primorial symmetric sequence: 5, 11, 17, 23, and 29, which can be obtained also from Equation 15.

$6\cdot n+1\text{ (14)}$

$6\cdot n+5\text{ (15)}$

Multiplying by five the unfolded elements of the OP, the first elements to remove from the pre-5-PPS are obtained. The only value below 30 is 5, so it will be removed. By primorial symmetry, 25 (30 - 5 = 25) is removed too. The removal of 25 will create a CP, defined by Equation 16. The CP will have a phase equal to the number removed, 25, and a multiplicative factor equal to the primorial of the Prime Number defining the PPS, 30.

$30\cdot n+25\text{ (16)}$

Removing Equation 16 from Equation 14 results in the OP defined by 5-PPS (Equation 17). The first elements obtained from the development of the OP are the members of the 5-PPS as well as the phases of the OP.

$\mathrm{<mo\; stretchy="false">(</mo>6}\cdot n+\mathrm{1<mo\; stretchy="false">)</mo>}-\mathrm{<mo\; stretchy="false">(</mo>30}\cdot n+\mathrm{25<mo\; stretchy="false">)</mo><mo>=</mo>}\{\begin{array}{ll}\hfill & 30\cdot n+\mathrm{1<mo>=</mo>1,31,61,...}\hfill \\ \hfill & 30\cdot n+\mathrm{7<mo>=</mo>7,37,67,...}\hfill \\ \hfill & 30\cdot n+\mathrm{13<mo>=</mo>13,43,73,...}\hfill \\ \hfill & 30\cdot n+\mathrm{19<mo>=</mo>19,49,79,...}\hfill \end{array}\text{ (17)}$

The only OP not included is the one with phase 25. The removal of 25 is due to the effect of an element of the symmetric series (Equation 15). The criteria to define which series should be removed is fulfilled only by the series defined by Equation 16. It is a CP, and Prime Numbers will not be allocated in this path.

Symmetry hypothesis: The properties of a number are shared by its primorial symmetric equivalent. If a number is a member of an x-PPS, its primorial symmetric equivalent is also a member. If it is not, the primorial symmetric equivalent is also not a member of the x-PPS.

Seven

The OP of the 5-PPS (Equation 17) is unfolded up to 210 to obtain the list of possible candidates for the 7-PPS. Multiplying by seven the unfolded elements of the OP, the first elements to remove, those lower than 210, from the 7-PPS are obtained. For example, the 5-PPS primorial OP (Equation 18) is developed up to the primorial of seven: 31, 61, 91, 121, 151 and 181. The only element to remove is 91 (7 × 13). 91 is not an element of the 7-PPS and is the phase of one of the 7-PPS CP.

$30\cdot n+1\text{ (18)}$

$210\cdot n+91\text{ (19)}$

The calculated CP (Equation 19) is subtracted from the primorial 5-PPS OP (Equation 18), obtaining the new 7-PPS OP (Equation 20):

$30\cdot n+1-210\cdot n+\mathrm{91<mo>=</mo>}\{\begin{array}{ll}\hfill & 210\cdot n+1\hfill \\ \hfill & 210\cdot n+31\hfill \\ \hfill & 210\cdot n+61\hfill \\ \hfill & 210\cdot n+121\hfill \\ \hfill & 210\cdot n+151\hfill \\ \hfill & 210\cdot n+181\hfill \\ \hfill & \hfill \end{array}\text{ (20)}$

The same process is done on the remaining 5-PPS OP, obtaining the complete 7-PPS. The process can also be partially done to half of the OP as explained before, obtaining the remaining elements by primorial symmetry. Equation 21 shows the symmetric results of Equation 20. For instance, the CP with phase 91 has its symmetric CP with phase 119 (210 - 91 = 119). The same applies to the OP.

$30\cdot n+29-210\cdot n+\mathrm{119<mo>=</mo>}\{\begin{array}{ll}\hfill & 210\cdot n+209\hfill \\ \hfill & 210\cdot n+179\hfill \\ \hfill & 210\cdot n+149\hfill \\ \hfill & 210\cdot n+89\hfill \\ \hfill & 210\cdot n+59\hfill \\ \hfill & 210\cdot n+29\hfill \\ \hfill & \hfill \end{array}\text{ (21)}$

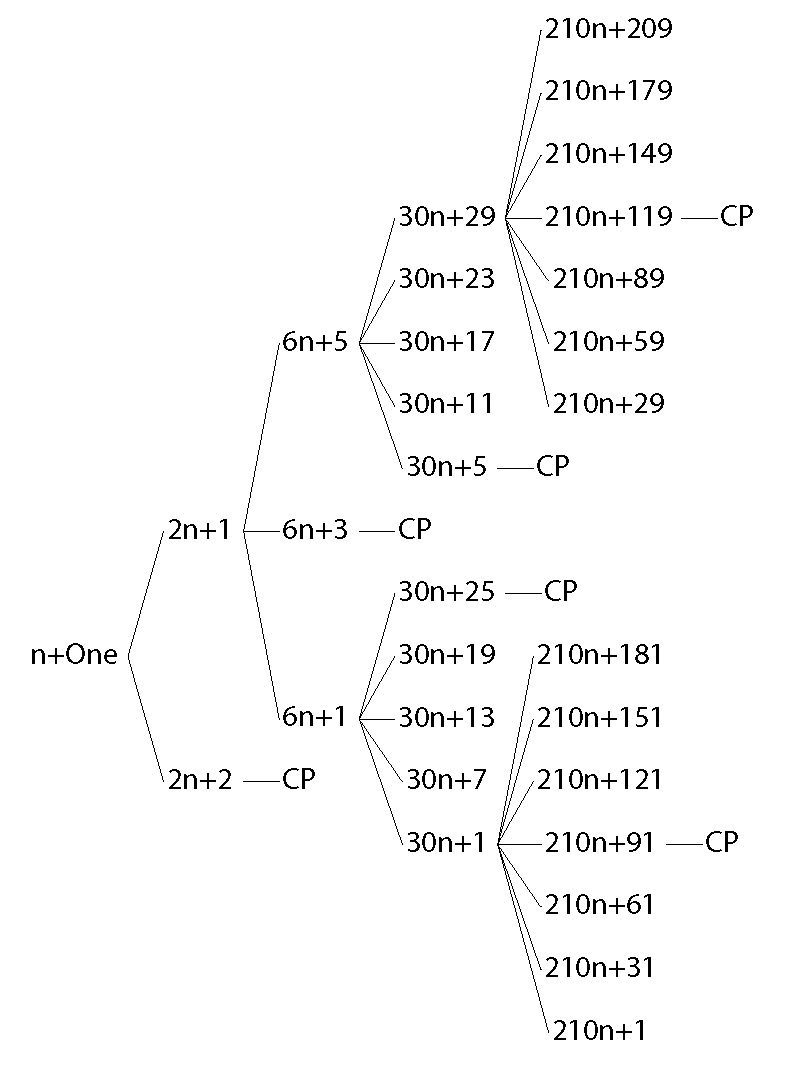
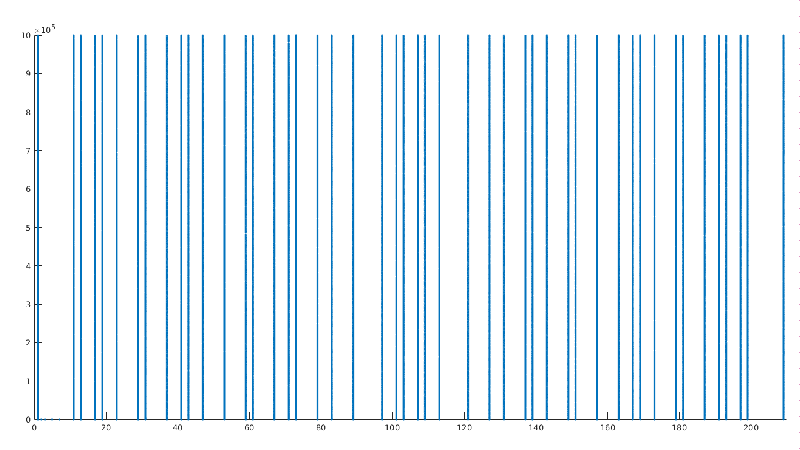
In the same way, it can be obtained the 7-PPS elements from the remaining 5-PPS. Once all the 7-PPS elements have been obtained, it is possible to pass them to the next PPS. The unfolding of the 7-PPS is shown in Figures 4-6. It can be seen in the replicas of the 5-PPS, plus the variation added by seven (the CP, which effect increases the spacing between some OP). The spacing between the vertical lines of the figure matches exactly the pattern defined by the 7-PPS. Another interesting detail is the presence of 121, 169, and 209 in the 7-PPS. As it has already been explained, the composites of a higher order than the PPS being evaluated are members of the PPS as well as the phases of OP. Also, it is possible to see that the Prime Numbers lower than the PPS being evaluated are CP. Figure 4 shows the expanded tree of OP up to PPS-7. The summary of the first PPS, up to 41-PPS, including the primorial, the number of total paths, OP, and CP is presented in Table 1.

Perfect composite hypothesis: A Composite Number of a higher order than the PPS, if it is lower than the length of the PPS, will be a member of the PPS and will be the first element or phase of an OP. As already explained it will be called a Perfect Composite.

Perfect prime gap: The Prime Numbers lower than the Prime Number defining a PPS are CP, defining a Prime Gap with a minimum length equal to the distance from one to the next Prime Number. It will be defined as PPG. The first PPG is observed in the first replica of the PPS while the mirrored PPG is first observed in the PPS definition itself. The 7-PPG is observed in Figure 6.

Perfect space hypothesis: There are as many PS as there are combinations of Prime Numbers. They will provide different OP but the overall result will be the same.

Practice

Getting prime numbers

A very rudimentary algorithm has been implemented based on the Open Path Theory described in the previous Section. The algorithm navigates from one OP of one PPS to another OP of the consecutive PPS performing the appropriated transformation. It only chooses one OP, for instance, always right in the next transformation. The algorithm, which Matlab code is presented below, starts with the 30 . n+1 OP (obtained from the development of the 6 . n+1 OP) and iterates performing the transformation that has been exemplified through the previous Section, but choosing only one OP at each iteration.

Several iterations are done and a sample of numbers is obtained, harvesting the OP that calculates the algorithm.

[language = Matlab]images/search_primes.m

Finding two divisors of a PS member

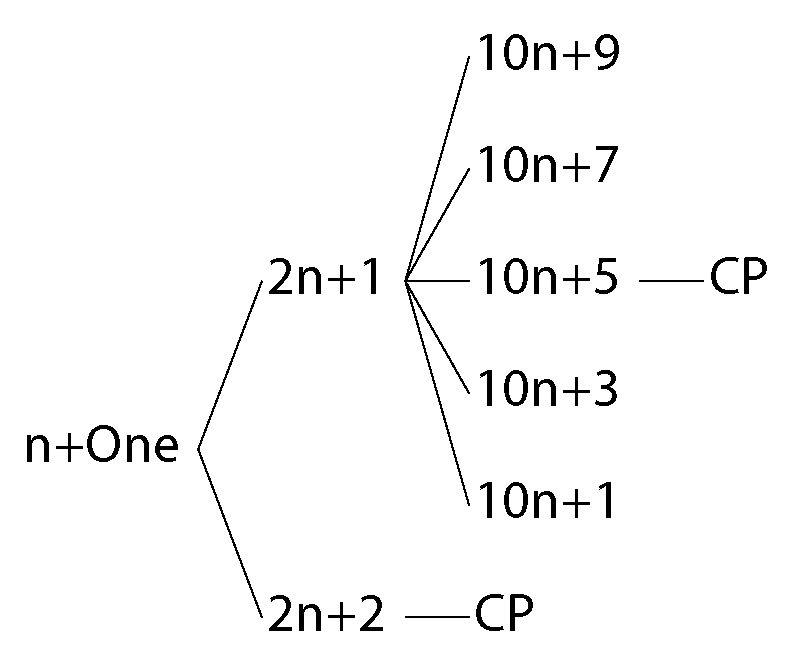
An OP determines a series where Prime Number coexists with composite numbers. The following method can be used to determine if a number is composite, and if it is so, it provides two numbers for which multiplication gives the number evaluated. The method can be used with any PPS. It will be provided several examples for the PS created with Prime Numbers 2 and 5 and also for 17-PPS. A number in an OP is composite if there exist two numbers of the OP of its PPS that multiplied by themselves give the number. In the case of the PS of 2 and 5, the length of the PS is 10. There exist four OP, defined by the series 10 . n+1, 10 . n+3, 10 . n+7, and 10 . n+9. The OP of this PS explains why there are only Prime Numbers ending in 1,3,7 and 9. Figure 7 shows the tree describing the PS(2,5).

A composite number in an OP will always result from the multiplication of elements of determined and known-in-advance OP. For the PS(2,5), the OP 10 . n+1 member will result from the multiplication of two elements of OP 10 . n+1, two elements of OP 10 . n+9 or one element from the OP 10 . n+7 and another one from the OP 10 . n+3. So an element in OP 10 . n+1 will be either a Prime Number or a composite of two numbers with the previous combinations. Equation 22 presents all the different possibilities for PS(2,5). The study of such equations can provide further information about the density of Prime Numbers.

$\begin{array}{l}10\cdot p+1\stackrel{}{\to }\mathrm{<mo\; stretchy="false">(</mo>10}\cdot n+\mathrm{1<mo\; stretchy="false">)</mo>}\cdot \mathrm{<mo\; stretchy="false">(</mo>10}\cdot m+\mathrm{1<mo\; stretchy="false">)</mo><mo>|</mo><mo>|</mo><mo\; stretchy="false">(</mo>10}\cdot n+\mathrm{3<mo\; stretchy="false">)</mo>}\cdot \\ \mathrm{<mo\; stretchy="false">(</mo>10}\cdot m+\mathrm{7<mo\; stretchy="false">)</mo><mo>|</mo><mo>|</mo><mo\; stretchy="false">(</mo>10}\cdot n+\mathrm{7<mo\; stretchy="false">)</mo>}\cdot \mathrm{<mo\; stretchy="false">(</mo>10}\cdot m+\mathrm{3<mo\; stretchy="false">)</mo><mo>|</mo><mo>|</mo><mo\; stretchy="false">(</mo>10}\cdot n+\mathrm{9<mo\; stretchy="false">)</mo>}\cdot \mathrm{<mo\; stretchy="false">(</mo>10}\cdot m+\mathrm{9<mo\; stretchy="false">)</mo>}\\ 10\cdot p+3\stackrel{}{\to }\mathrm{<mo\; stretchy="false">(</mo>10}\cdot n+\mathrm{1<mo\; stretchy="false">)</mo>}\cdot \mathrm{<mo\; stretchy="false">(</mo>10}\cdot m+\mathrm{3<mo\; stretchy="false">)</mo><mo>|</mo><mo>|</mo><mo\; stretchy="false">(</mo>10}\cdot n+\mathrm{3<mo\; stretchy="false">)</mo>}\cdot \\ \mathrm{<mo\; stretchy="false">(</mo>10}\cdot m+\mathrm{1<mo\; stretchy="false">)</mo><mo>|</mo><mo>|</mo><mo\; stretchy="false">(</mo>10}\cdot n+\mathrm{7<mo\; stretchy="false">)</mo>}\cdot \mathrm{<mo\; stretchy="false">(</mo>10}\cdot m+\mathrm{9<mo\; stretchy="false">)</mo><mo>|</mo><mo>|</mo><mo\; stretchy="false">(</mo>10}\cdot n+\mathrm{9<mo\; stretchy="false">)</mo>}\cdot \mathrm{<mo\; stretchy="false">(</mo>10}\cdot m+\mathrm{7<mo\; stretchy="false">)</mo>}\\ 10\cdot p+7\stackrel{}{\to }\mathrm{<mo\; stretchy="false">(</mo>10}\cdot n+\mathrm{1<mo\; stretchy="false">)</mo>}\cdot \mathrm{<mo\; stretchy="false">(</mo>10}\cdot m+\mathrm{7<mo\; stretchy="false">)</mo><mo>|</mo><mo>|</mo><mo\; stretchy="false">(</mo>10}\cdot n+\mathrm{3<mo\; stretchy="false">)</mo>}\cdot \\ \mathrm{<mo\; stretchy="false">(</mo>10}\cdot m+\mathrm{9<mo\; stretchy="false">)</mo><mo>|</mo><mo>|</mo><mo\; stretchy="false">(</mo>10}\cdot n+\mathrm{7<mo\; stretchy="false">)</mo>}\cdot \mathrm{<mo\; stretchy="false">(</mo>10}\cdot m+\mathrm{1<mo\; stretchy="false">)</mo><mo>|</mo><mo>|</mo><mo\; stretchy="false">(</mo>10}\cdot n+\mathrm{9<mo\; stretchy="false">)</mo>}\cdot \mathrm{<mo\; stretchy="false">(</mo>10}\cdot m+\mathrm{3<mo\; stretchy="false">)</mo>}\\ 10\cdot p+9\stackrel{}{\to }\mathrm{<mo\; stretchy="false">(</mo>10}\cdot n+\mathrm{1<mo\; stretchy="false">)</mo>}\cdot \mathrm{<mo\; stretchy="false">(</mo>10}\cdot m+\mathrm{9<mo\; stretchy="false">)</mo><mo>|</mo><mo>|</mo><mo\; stretchy="false">(</mo>10}\cdot n+\mathrm{3<mo\; stretchy="false">)</mo>}\cdot \\ \mathrm{<mo\; stretchy="false">(</mo>10}\cdot m+\mathrm{3<mo\; stretchy="false">)</mo><mo>|</mo><mo>|</mo><mo\; stretchy="false">(</mo>10}\cdot n+\mathrm{7<mo\; stretchy="false">)</mo>}\cdot \mathrm{<mo\; stretchy="false">(</mo>10}\cdot m+\mathrm{7<mo\; stretchy="false">)</mo><mo>|</mo><mo>|</mo><mo\; stretchy="false">(</mo>10}\cdot n+\mathrm{9<mo\; stretchy="false">)</mo>}\cdot \mathrm{<mo\; stretchy="false">(</mo>10}\cdot m+\mathrm{1<mo\; stretchy="false">)</mo>}\text{ (22)}\end{array}$

$10\cdot p+\mathrm{1<mo>=</mo><mo\; stretchy="false">(</mo>10}\cdot n+\mathrm{1<mo\; stretchy="false">)</mo>}\times \mathrm{<mo\; stretchy="false">(</mo>10}\cdot m+\mathrm{1<mo\; stretchy="false">)</mo><mo>=</mo>100}\cdot n\cdot m+10+10\cdot m+1\text{ (23)}$

If the first of the possible combinations are taken and developed (Equation 23), it is observed that the second part of the Equation is also part of the OP 10 . n+1, so they can be reorganized to fit it (Equation 24):

$10\cdot p+\mathrm{1<mo>=</mo>10}\cdot \mathrm{<mo\; stretchy="false">(</mo>10}\cdot n\cdot m+n+m\mathrm{<mo\; stretchy="false">)</mo>}+1\text{ (24)}$

dividing by 10 the remainder is 1 while the quotient is:

$p\mathrm{<mo>=</mo>10}\cdot n\cdot m+n+m\text{ (25)}$

Dividing again by 10:

$p\mathrm{mod}\mathrm{10<mo>=</mo>}n+m\text{ (26)}$

$di{v}_{10}\mathrm{<mo\; stretchy="false">(</mo>}p\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}n\cdot m\text{ (27)}$

This is always true if n + m is lower than 10. If it is bigger than 10, then it has to be adjusted by decreasing div10 (p) by one and increasing p mod 10 by 10 as many times as needed to find a natural solution to the equation system. If in this process a natural solution is found, then 10 . p+1 is a composite number and n and m provide a couple of numbers that are divisors of the number evaluated. If there is no solution in any of the different OP combinations, then, the number is prime. Let's see it with a couple of examples (only checking the first of the OP possibilities)

Example I: 341 in the PS (2,5): 341 is a composite number that comes from 11 × 31. It is also a component of the OP 10 . n+1. The equation system is prepared following the process indicated in the previous Subsection and presented in Equation 28:

$\{\begin{array}{ll}\hfill & 34\mathrm{mod}\mathrm{10<mo>=</mo>}n+m\mathrm{<mo>=</mo>4}\hfill \\ \hfill & di{v}_{10}\mathrm{<mo\; stretchy="false">(</mo>34<mo\; stretchy="false">)</mo><mo>=</mo>}n\cdot m\mathrm{<mo>=</mo>3}\hfill \end{array}\text{ (28)}$

Without performing any iteration the equation system has a natural solution:

$\{\begin{array}{ll}\hfill & n\mathrm{<mo>=</mo>1}\hfill \\ \hfill & m\mathrm{<mo>=</mo>3}\hfill \end{array}\text{ (29)}$

341 is not a Prime Number and it results from the multiplication of (10 . 1+1) . (10 . 3+1) = 11 31.

Example II: 4331 in the PS (2,5): 4331 is a composite number that comes from 61 71 and it is also a component of the OP 10 . n+1. Again the equation system is prepared and it is presented in Equation 30:

$\{\begin{array}{ll}\hfill & 433\mathrm{mod}\mathrm{10<mo>=</mo>}n+m\mathrm{<mo>=</mo>3}\hfill \\ \hfill & di{v}_{10}\mathrm{<mo\; stretchy="false">(</mo>433<mo\; stretchy="false">)</mo><mo>=</mo>}n\cdot m\mathrm{<mo>=</mo>43}\hfill \end{array}\text{ (30)}$

The equation system has not a natural solution, so it is needed to update Equation 30 as explained before, obtaining Equation 31:

$\{\begin{array}{ll}\hfill & 433\mathrm{mod}\mathrm{10<mo>=</mo>}n+m\mathrm{<mo>=</mo>13}\hfill \\ \hfill & di{v}_{10}\mathrm{<mo\; stretchy="false">(</mo>433<mo\; stretchy="false">)</mo><mo>=</mo>}n\cdot m\mathrm{<mo>=</mo>42}\hfill \end{array}\text{ (31)}$

Now the equation system has a natural solution:

$\{\begin{array}{ll}\hfill & n\mathrm{<mo>=</mo>6}\hfill \\ \hfill & m\mathrm{<mo>=</mo>7}\hfill \end{array}\text{ (32)}$

4331 is not a Prime Number and it results from the multiplication of (10 . 6+1) (10 . 7+1) = 61 71.

Example III: 390553184396891 in the PS (2,5): 390553184396891 is a composite number that comes from the multiplication of two Prime Numbers: 15487061 and 25218031. It is also a component of the OP 10 . n+1.

$\{\begin{array}{ll}\hfill & 39055318439689\mathrm{mod}\mathrm{10<mo>=</mo>}n+m\mathrm{<mo>=</mo>9}\hfill \\ \hfill & di{v}_{10}\mathrm{<mo\; stretchy="false">(</mo>39055318439689<mo\; stretchy="false">)</mo><mo>=</mo>}n\cdot m\mathrm{<mo>=</mo>3905531843968}\hfill \end{array}\text{ (33)}$

The equation system (Equation 33) has not a natural solution, so it is needed to update it as explained before for 407050 iterations. In this case, the first 395000 iterations have a complex solution so it is possible to quickly jump to the real solutions. 12000 iterations are needed to find the natural solution. The other three possible equation systems need to be evaluated as well. They will not provide a natural solution. In the 2-PPS there is only one equation system to solve and the solution requires 10176272 iterations, of which 295072 correspond to real solutions.

The examples presented are very simple. It is expected that for PPS of higher order, the number of iterations will decrease and the number of different OP possibilities will increase (one per OP). The problem is segmentable, which would allow the use of devices such as FPGAs to speed up the resolution of the problem.

Example IV: 390553184396891 in the 17-PPS: The 17-PPS has 92160 OP and a length of 510510 elements. The total number of equation systems to evaluate will be the number of OP. It will be presented only the equation system set that provides the only natural solution. The equation that defines the multiplication is:

$510510\cdot p+\mathrm{55571<mo>=</mo><mo\; stretchy="false">(</mo>510510}\cdot n+\mathrm{171761<mo\; stretchy="false">)</mo>}\times \mathrm{<mo\; stretchy="false">(</mo>510510}\cdot m+\mathrm{203041<mo\; stretchy="false">)</mo>}\text{ (34)}$

being one of the 92160 possible equation combinations. The equation system is the one presented in Equation 35:

$\{\begin{array}{ll}\hfill & f^{\prime }\mathrm{<mo>=</mo>203041}\cdot n+171761\cdot m+\mathrm{68316<mo>=</mo>281552}\hfill \\ \hfill & p^{\prime }\mathrm{<mo>=</mo>}n\cdot m\mathrm{<mo>=</mo>1948}\hfill \end{array}\text{ (35)}$

The first equation system does not have a natural solution, nor a real one. The natural solution is found at iteration 28, the first of the real solutions.

Results and discussion

The OP Theory has been presented as being possible to determine the series to which the Prime Numbers are restricted. The algorithm proposed in Section 3 navigates, without a clear space direction, through one of the many OP that a PPS defines. Navigating up to the 29-PPS, a sample of a few hundredths of numbers is obtained with ratios of coincidence of 0.278 (27.8%). For the mirror image, the ratio obtained is 0.268. The values returned by the algorithm are in the 1.0e+11 region. The results with the load OP [1 7 13 19], and always turning right in a bifurcation are presented in Table 2. The samples are obtained at distances higher than 1011. The second algorithm, presented in Subsection 3.2, provides a method to evaluate if a number is composite or prime.

The OP Theory also predicts regions in the space that will not have any Prime Number. The bigger of the regions is called Perfect Primorial Gap and in order to determine it only one is needed to know the Primorial. Other gap regions can be found by analyzing the PPS structure. In the case of using a PS instead of a PPS, the primorial gap will not exist and the gap regions should be obtained from the PS structure.

Conclusion

In this current article, a groundbreaking theory is introduced, offering fresh insights into the intricate pattern and structure governing the distribution of prime numbers. This theory is firmly rooted in three key concepts: Perfect Space, Primorial Perfect Space, and Open Paths. By delving into these concepts, the article seeks to provide a more comprehensive understanding of how prime numbers are distributed within the realm of natural numbers. At the core of this theory is the notion of the "Perfect Space," which represents a novel perspective on the spatial arrangement of prime numbers. It explores the idea that prime numbers may exhibit a previously unrecognized order within the vast landscape of natural numbers. This concept serves as the foundation upon which the subsequent ideas are built. The concept of "Primorial Perfect Space" takes this exploration even further by introducing a more refined framework. It delves into the notion that certain prime numbers, possibly those with unique characteristics or properties, may occupy a distinct and highly structured space within the number line.

Furthermore, the article goes beyond theoretical considerations and presents two algorithms, albeit in their rudimentary form. These algorithms serve as empirical tools to test and validate the proposed theory. By applying these algorithms to real-world data or simulated scenarios, the article seeks to provide tangible evidence that supports the theory's validity. While these algorithms may be in their infancy, they represent a promising step towards verifying the theory's correctness or, at the very least, its alignment with the true nature of prime number distribution.

In essence, this article represents a pioneering endeavor to uncover the hidden order within the prime number distribution. Introducing innovative concepts and empirical approaches sets the stage for further exploration and refinement of our understanding of prime numbers and their spatial arrangement in the realm of natural numbers. While the theory may be a work in progress, it is an exciting and open path that holds the potential to revolutionize our comprehension of this fundamental aspect of number theory.

1. Havil J, Gamma J. Exploring euler’s constant. 2003 .
2. Granville A. Harald Cramer and the distribution of prime numbers, Scandinavian Actuarial Journal. 1995; 1:12–28.
3. Cranball R. Cranball CPR. Prime Numbers A Computational Perspective. Springer, 2005.
4. Green B, Tao T. The primes contain arbitrarily long arithmetic progressions, Ann Math.2004; 167. doi 10.4007/annals.2008.167.481.
5. Porras J, Andrade C. The formation of prime numbers and the solution for Goldbach's conjectures, World Open Journal of Advanced Mathematics. 2014; 2:1–32.
6. Porras J, Ferreira P. The pattern of prime numbers, Applied Mathematics. 08, 2017; 180–192. doi: 10.4236/am.2017.82015 .