Annals of Mathematics and Physics
All physical information is discretely connected from the beginning and all geometrical appearance is a delayed statistical consequence
Wolfgang Orthuber*
Cite this as
Orthuber W (2023) All physical information is discretely connected from the beginning and all geometrical appearance is a delayed statistical consequence. Ann Math Phys 6(2): 159-172. DOI: 10.17352/amp.000097Copyright Licence
© 2023 Orthuber W. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.Information is physically measurable as a selection from a set of possibilities, the domain of information. This defines the term "information". The domain of the information must be known together reproducibly beforehand. As a practical consequence, digital information exchange can be made globally efficient, interoperable, and searchable to a large extent by online definition of application-optimized domains of information. There are even more far-reaching consequences for physics. The purpose of this article is to present prerequisites and possibilities for a physical approach that is consistent with the precise definition of information. This concerns not only the discretization of the sets of possible experimental results but also the order of their definition over time. The access to or comparison with the domain of information is more frequent, the earlier it was defined. The geometrical appearance of our space is apparently a delayed statistical consequence of a very frequent connection with the common primary domain of information.
1. Introduction: The domain of information
The basis of the approach presented here is the exact definition 1.1 of information as a selection from a commonly known (finite) set (the domain of information). This is new and could trigger a controversial debate. For example, every meter of distance that we together can measure is due to this definition considered a discrete common set of possibilities for physical information. Such a consistent information-theoretic basis of physics is missing so far. So the use of a priori infinite sets (e.g. of continuous numbers) is widespread, but not consistent with the definition 1.1. If someone wants to ignore definition 1.1, he/she should provide a well-defined (set theoretic) alternative to 1.1. Otherwise, it is clear: Since the information is a selection from the set of its possibilities (from the domain of information), and this set must be known beforehand (i.e. as part of finite past), in theoretical physics even a well-defined approach to real (finite) information and also to (in the past finite) time is required. The article shows approaches on how to get closer to the solution of this problem.
The importance of definition 1.1 arises from the fact that information is a fundamental part of our existence - information shapes our lives. Scientific disciplines such as information science and computer science deal with information processing. Nevertheless, the term "information" has not yet been precisely defined. Strictly speaking, the lack of an exact definition of information is a shortcoming (which also leads to critical literature [1,2]), because elementary information is by no means fuzzy: Physically, the transport of elementary information is done by energy quanta (this will be discussed further in section 3.7) or technically by "bits". Each bit means a selection from a set of 2 possibilities. Bits are used to encode numbers. These are selections from ordered sets, which can also be very large. Thus the conditions are given to start as sharp as usual in mathematics: with set theory. We know from mathematics that it is possible to build very complex and well-founded approaches starting from ordered sets. A systematic and efficient approach is thus made possible.
Digital and all other physical information is exchanged as the reproducible result of a (physical) measurement and represents no more and no less than a reproducible selection from the ordered set of all possible measurement results. This set of possibilities is the "domain" of information. The common order is necessary for reproducible selection. Thus, "information" can be considered as a result of a mathematical function. This function has a domain, and the function result is an element (the selected possibility) of the domain of information. This basic principle even defines information:
1.1 Theorem (Definition of information)
Information is a reproducible selection from its domain.
The domain of information (i.e. its selectable elements and their order) must be reproducibly known by all those exchanging the information, i.e. after a reproducible sequence of elementary steps, the information exchanged must be identical for all. From this follows also the finiteness of the domain (within finite time).
We can say abbreviated: The domain of information must be uniformly defined for all and is inseparable from the information. This principle is pervasive and substantially underestimated.
1.2 Digital application of the definition of information
The relevance of the exact definition 1.1 of information is obvious in computer science. We could apply it systematically and efficiently by using the Internet to define the domains of digital information globally in a uniform way for all users. Digital information is always a sequence of numbers, i.e. a selection from ordered sets. For example, we can start with sequences of "quantitative data" and optimize them for the application of interest. This has already been explained and described in detail [3]. The resulting exchanged binary information is called "domain vector" or "DV" and has the structure:
DV: UL plus UL plus number sequence
"UL" means "Uniform Locator" and is an efficient global pointer to the machine-readable online definition of the number sequence. The domain of the number sequence is thus automatically defined uniformly worldwide (as the domain of the transported information). In this way, interoperable and searchable digital information could be uniformly defined online worldwide. It would be optimizable for the respective application and precisely comparable and searchable. This is also demonstrated online. With respect to the digital application, essential conclusions are thus obvious: The data structure of the DV can efficiently encode all possible types of digital information and make them globally exchangeable, comparable, and searchable in an energy-saving manner.
Despite considerable technical, scientific, and economic importance, the (uniform) online definition of digital information (number sequences) has not yet been introduced. The alternative is the repeated non-uniform local definition in all possible formats - this is much less efficient, mostly not comparable, and thus incompatible ("non-interoperable"), it causes an enormous amount of unnecessary redundant work in programming and especially in application. Therefore, it would be appropriate to teach and systematically deepen the much more efficient uniform global (online) definition of digital information.
The systematic digital utilization of definition 1.1 is only one of many possible applications. A consequent analysis of 1.1 goes to the heart of the matter and can influence the worldview. Not only does it show that our frame of reference must be completely connected a priori, but it also shows combinatorial details. In [3] it was already briefly mentioned that 1.1 holds without exception. Since "information" is of central importance to us, so is its definition 1.1. Information and its domain even shape our consciousness. At this, the access (comparison with) the domain is mostly fast and unconscious. For example, language vocabulary as a common domain of linguistic information exchange must be quickly available or "familiar" to all communicators.
In general, it turns out that domains learned earlier usually allow faster access. Our brain learned the vocabulary of our body's nerve impulses early on and now uses this knowledge unconsciously and quickly. Later, it learned the signals of our environment. This also opens up possible applications in psychology - that would be another area that could be systematically expanded.
The basic principle 1.1 is superordinate. Everywhere where information plays a role (and these are many subject areas) applications can arise.
Strictly speaking, fundamental physics is the original science about information, because the result of every physical experiment is information and also means a selection from the set of possible experimental results. This is just the domain of the resulting information according to 1.1. In section 4.7 of [3], it was already mentioned that the (implicit) knowledge of the domain of information 1.1 and the resulting combinatorics is a far-reaching topic for research in physics.
This article shall therefore show prerequisites and first possibilities towards a physical approach, which is compatible with the exact definition 1.1 of information.
2. Materials and methods: Mathematical tools for the analysis of the domain of information
Until today, the consideration of the exact definition 1.1 of information has not been focused in physics. It has not been systematically explored why (together with relativity) there is always a common order of "time" for the exchange of information. Thus, this topic can be extended and can lead to surprising conclusions.
Naturally, definition 1.1 of information first concerns theoretical physics, especially quantum mechanics. The consequent application of 1.1 is very far-reaching, unusual, and new. Therefore, there is a danger that the arguments put forward here will not be taken seriously. On the other hand, it quickly becomes clear that silence does not provide a solution either because a convincing concept (even the definition of time) must be in accordance with 1.1. However, fundamental concepts commonly used in theoretical physics start from other basics than 1.1. Starting from the usual geometrical view, classical theoretical physics was first introduced. When this was no longer sufficient, quantum mechanics was developed. Here interesting and important relations were uncovered and more exactly analyzed how measured information influences the future entire (worldwide) reality. Also, Hilbert spaces were introduced, which are closed and separable [4], i.e. they contain a countable dense set and have a countable orthonormal basis. The term "countable" already implies a systematic constructability of the set. But still, a priori (time-independent) infinite sets are used, for example for the description of location and momentum, as it was common in classical geometrical concepts. These compromises were chosen because they were helpful in practice for a quick explanation of experimental results. The geometric view still plays an essential role, despite the experimentally detectable quantization of the exchanged energy measurable in experiments (ultimately as information). Note, that complex, hierarchical combinatorics and multidimensional, ever-increasing sets are not the problem. The problem lies in concepts (e.g. sets) that allow time-independent "existing" infinity. Continuous sets allow far too much freedom - without equivalent in reality. From the point of view of information theory, a priori infinite sets and thus the "real numbers" (routinely used in geometry) are completely incompatible with 1.1. Every finite interval of a continuous set different from 0 contains infinitely many elements independent of time. To "know" them, one needs an infinite amount of (ultimately undefined) information - such a thing is not real. The real numbers are helpful for many practical argumentations and are also necessary here for bridging existing constructs with analytic functions. But we must not forget: A priori infinite sets are only constructs and not bijectively mappable to something real. If we want to get much further in understanding reality, it is not enough that our mathematical model approximates experimental results. It must be discrete and it must be guaranteed that the size of the domains of the measurable information is only finite within finite measuring time. It is possible (and given the enormous size of the visible universe also plausible) that the size of the domains of information grows without limits, but only together with time. (Despite relativistic time dilation, macroscopic time reversal is not measurable, i.e. there is a common increase in time).
We therefore need a common concept of time increment that connects us for the transport and exchange of information, also because of 1.1. Here, a concept published years ago [5] can help, which, starting from the (measurable) "time dilation", provides a finite and quantitative approach to proper time as a "sum of return probabilities". There are several mathematical and structural connections and peculiarities here, which offer a starting point for the information-theoretical approach 1.1 but are still unconsidered in present approaches of theoretical physics. Bridging to common concepts of theoretical physics is possible by assuming that the common "set of possibilities" or domain of information per proper time grows only together with the (common) time. The elementary steps for this can be done with unbounded increasing frequency (in particular the access to the basic primary domain, cf. section 3.7) and require a new combinatorial approach to the concept of time. This is possible and it can be shown that essential current computational models (e.g. geometric functions like sin(x) and cos(x) and also their generalization by the (matrix) exponential function, cf. section 3.6) can be derived from it. In the following, it will be introduced and discussed step by step.
The present time separates between future and past time. Future means "no previous information". We first consider a basal experiment as simple as possible, which delivers exactly 1 bit of information without prior information, i.e. a selection from one of 2 possibilities, e.g. drawing one of two equally probable balls "1" or "-1" from an urn. For possibility "1" we move one step to the right, and for possibility "-1" to the left. Let k be the position to the right of the origin after n ≥ 0 steps. The integer k thus increases by 1 when drawing ball "1" and decreases by 1 when drawing ball "-1". This results in a so-called Bernoulli Random Walk or BRW with binomial distribution of the path possibilities.
Thus, n and k are integers with n≥0 and -n ≤ k ≤ n. The well-known Pascal's triangle or binomial distribution (Table 1) shows, as a function of the number of steps n, the number of path possibilities towards position k. These correspond to the binomial coefficients:
The column k=0 plays a special role. It represents the number of return possibilities to the origin k=0. Without prior information (unknown future) steps to the right and the left have equal probability p=1/2. In this column, k=0 is also the symmetry center. Since this choice of this "coordinate system" (n, k) has many advantages and reveals interconnections, we define the resulting symmetric probability distribution as a function:
The function Q0 represents probabilities in the symmetric BRW. It holds:
Equation (3) shows the algorithm of the symmetric BRW. We can also define the general function Q with the general basic algorithm:
Here Q(n, k)=0 for |k|>n. In the case we can consider ank and bnk as probabilities. In the general case, ank and bnk are constant factors, which can be called probability amplitudes for steps to the right and left. These can also be complex numbers or, more generally, matrices or linear operators, as is common in quantum mechanics. Obviously, (4) also applies to all linear combinations or superpositions:
The summation can also be performed only over a partial range, e.g. only over one step (i.e. fixed n, e.g. n=nmax) or overstep sequences with different frequencies, depending on the proper time (8). Essential is the uniform definition of n and k and their basal synchronization, so that ank and bnk have constant meaning until the summation is finished. The general function Q(n, k) from (4) is defined only together with the factors ank and bnk. These must be fixed before. The laws, which follow from the algorithm (4), are valid for all linear combinations of Q(n, k) and Q0(n, k). Certain combinations (4) and (5) in analytic models with continuous sets of numbers result in derivatives and integrals. In the following, for the sake of clarity, simple definitions will be chosen, e.g. ank = bnk 1/2. In this constant symmetric case Q(n, k) = Q0(n, k) is valid. The function Q0(n, k) already has many interesting properties and is broadly combinable (5). This may be a reason for the universality of the Schrödinger equation, cf. Section 3.5.
By induction, we obtain [5]:
The physical relevance is first shown in a context that has already been described and derived in detail [5]: We experiment with an inertial frame of reference. Let c be the velocity of light, v the velocity of a clock relative to the observer in an inertial frame, and let x=v/c be the ratio to the velocity of light. According to the experimentally measurable relativity, the function f0(x) (7) shows the time dilation:
That means the moving clock goes slower than the observer's clock by the factor f0(x). The Taylor series expansion of this function f0(x) is:
The last line (8) illustrates the relationship of time dilation with the return probabilities when compared with Table 1 in k=0. Time dilation corresponds to the sum of the return probabilities of a BRW with probabilities p=(1-√(1-x2))/2 for a step to one side and p=(1+√(1-x2))/2 for a step to the other side. "Time" thus shows itself proportional to the number of return events. The symmetric case p=1/2 for both sides is particularly interesting. This case occurs in the case x=1 or v=c and is thus the rule for electromagnetic interaction. This transports information and here we need an exact information theoretic calculation, but just in this typical case, the analytic expression (7) for the time dilation is not usable and infinite (a priori, thus not conforming to reality). On the other hand, the sum (8) is also possible for x=1 over a finite (increasing) number of steps and thus can be also finite within finite time. Therefore, in the following, we assume that the approach of a BRW (progressing with each increase of time) actually provides deeper insights into the combinatorics of reality and we will get a confirmation for this.
Also important are linear superpositions or combinations of BRWs and their derivatives: As shown in (5), BRWs can also be superimposed with different prefactors (linear), for example with different signs (due to a conservation law). Table 2 shows a simple example of a superposition of two BRWs with opposite signs, which start with 1 in n=1 and k=-1 and with -1 in k=1. Because of this antisymmetric start and (3), the value 0 results in column k=0 for all n. In addition, antisymmetric values with opposite signs result for k<0 and k>0. Table 2 shows this.
We can also consider such a superposition as in Table 2 as the first discrete derivative along k. We define the discrete derivative QD(d, n, k) of degree d by QD(0, n, k) = Q0(n, k) and for n≥d≥1.
Here n ≥ d is necessary to have enough values at all to form finite differences of d-th order. This only becomes apparent in the discrete approach. For abbreviation let Q1(n, k)=QD(1,n,k) and Q2(n, k)=QD(2,n,k). The discrete derivatives (9) defined in this way can be calculated. In particular
The derivatives, such as (10) and (11), yield polynomials as prefactors. Similarly, Hermite polynomials result when using the exponential function as the generating function [6].
Table 2 shows up to n=6 the values of the first discrete derivative with respect to dk, i.e. the values of Q1(n, k). Because of exact antisymmetry around the middle column k=0, in rows 2n-1 at k= ±1 are the "flowing out" amounts, which according to (11) just correspond to the 2nd derivative Q2(2n, 0). These show up as coefficients of the Taylor series expansion of the function 1/f0(x) (8):
According to algorithm (3), a new row n+1 is created in each step (as in Table 1) and each value in position k is created by adding the neighboring values of the previous row n from position k-1 and k+1. Starting from this elementary simple algorithm, deeper insights are possible, also regarding the growth of the domain of information together with time. Therefore, we will now address some possibilities for this and show the first results.
3. Results: New approaches and implications
3.1 Eigentime as a finite sum
In the case of equal probability p=1/2 for steps to the right and to the left, the sum (8) of the return probabilities in k=0 grows with the number of steps n without limit. With the help of the Stirling formula and (6) holds for large n [5]:
With (6) follows
Thus we have for the time dilation at v=c the expression (14), which depends only on the number of steps of a symmetric BRW.
The function f0(x) (8) and its reciprocal (12) occur often in geometry and physics. With (14) we have a closed form also for the frequent case x=1 (resp. v=c). This is compatible with the definition of information 1.1 if we assume that the sum of the return probabilities (14) (and thus also the possible number of return events) at a given time is finite because it grows only together with time.
3.2 Estimation of the basal number of steps with access to the primary domain in this universe
The earlier a domain is defined, the more frequently it is accessed. This can be explained by the fact that domains defined earlier are also used for the definition of domains defined later. The access to the "primary domain" defined earliest at the time of origin of our universe occurs therefore maximally fast in (the part of the totality that we call) this universe, i.e. at every progress of our measurable time (this progress occurs for all of us at every exchange of energy quanta or photons, see also section 3.7). If we assume that also this common maximum measurable time progress occurs proportionally to the sum of the return probabilities of a primary BRW (which started in the symmetry center at the time of origin of our universe), we can try a first estimation of the so far occurred "maximum" number of steps nmax. For this, we assume that the maximum measurable expansion of the universe is proportional to the total expansion of the primary central BRW. Because of its large step number, the maximum probabilities of this BRW are meanwhile concentrated to only a small "pointed" range, since the standard deviation of a BRW grows only proportionally to the root of the step number n. What physical interactions might give a clue to this?
Interactions with limited ranges such as the weak and strong interactions come into question. The strong interaction is the strongest fundamental force in nature. In this rough estimate, let us first assume that the range of the strong interaction with about 10-15m [7] corresponds to the standard deviation of the primary BRW (connecting in our observable universe) and that the estimated "diameter" of about 8.8*1026 m of this universe [8] corresponds to the total extent or step number of the primary BRW. Then we get
In view of this rough estimate, it is remarkable for comparison that the number of photons of the extragalactic background radiation (EBL) [9] was estimated to be 4*1084, thus having a similar order of magnitude as nmax (15). If we (roughly) distribute the number nmax to the estimated age of this universe of 13.8 * 109 years or 4.35 * 1017 seconds, we get the following step frequency fmax:
fmax = nmax / 4.35 * 1017 = 1.78·1066 /s (16)
This frequency is very high. In comparison, the speed of light c is slow. From one step to the next, the light covers only the following distance smin:
smin = c / fmax = 3 * 108 m/s / 1.78·1066 /s = 1,68 * 10-58 m (17)
Thus, the range of the strong interaction or the diameter of an atomic nucleus with 10-15 m is about 1043 times larger than smin. Obviously, the gradation smin is much too fine to be measurable, giving the impression of a "continuum".
So, even the rough calculation (15) leads to very high frequencies for which our perceptible time, the speed of light, and therefore also our maximum information speed is only slow. This means that the information of all physical (external) measurements comes clearly delayed and therefore more or less from the past, depending on the proper time (14). The number of possibilities can grow extremely fast along a rare (under more preconditions later starting) proper time because of the fast increase in fmax (16) of the global number of steps (15).
It should be noted at this point that the standard deviation of a simple BRW is a simplification. For example, the superposition of two BRWs with opposite signs, starting from an original center k=0 as in Table 2, is plausible due to the conservation of energy. But also in this case (which also requires other renormalization) the resulting expansion and the distance of the extrema have similar magnitudes.
How can this now be fitted into the framework of quantum mechanics?
3.3 First bridge to quantum mechanics
Especially in quantum mechanics, the "information" of measurement results is shown to be crucial for future measurement results - thus ultimately for physics. The experimental results thus prove that we need a precise information-theoretical approach. Also, quantum physical experiments are particularly suitable for analyzing the combinatorics of information, because the set of possible measurement results of quantum physical experiments and thus the domain of generated information are clearly defined and manageable.
In quantum mechanics, physical states [10] are described by complex-valued vectors. The column vectors are called Kets and the corresponding complex conjugate row vectors Bras. Eigenstates of the system are basis states. These are described in each case by orthonormal basis vectors. This can result in high-dimensional state vectors already in the microscopic quantum physical domain. In current approaches, continuous result sets are assumed for, among others, location and momentum, resulting in infinite-dimensional state spaces containing all possible state vectors. In an (exact) information-theoretic approach, this must be replaced by finite-dimensional spaces. However, their dimensionality resp. the number of possibilities can grow extremely fast along proper time and can be synchronized for information exchange within the global step number (15). Even the rough calculation (15) leads to very high frequencies for which our perceptible time, the speed of light, and therefore also our information speed are very slow. This means that the information on physical measurements mostly comes from a clear past. This illustrates that a lot can happen during the measurement.
In (8), proper time was represented as the sum of return probabilities of a BRW. Each BRW up to the return in k=0 in line 2n can be decomposed into 2 BRWs in succession, each up to line n. For such "outward and return paths" there are several possibilities per return. Thus we get
Every progress of time is coupled with such return events according to (8). Progress of time is also coupled with every physical measurement. From this point of view, it is less surprising that the probability of every quantum mechanical measurement results from the product of a probability amplitude ("way there") with its complex conjugate ("way back") like in (18). Both are prerequisites for complete measurement which also implies time progress.
This view can also show a first bridge to geometry as a statistical consequence:
3.4 About statistics and geometry
We could consider a BRW from start to return (over positive k) as coupled with a mirrored BRW on the opposite side (over negative k) for reasons of symmetry. However, the exact information about the coupling is not necessarily available, perhaps only as an average value resulting from a conservation law. This may give the impression of a modified probability distribution with 2 independent BRWs, one over k<0 to Q0(n-1,-1) and one over k>0 to Q0(n-1,1). From there, the two seemingly independent BRWs each go to k=0 with probability 1/2. The probability Q0AND(n, 0) for this is then:
The meeting probability Q0AND(n, 0) of two simultaneously starting independent BRWs after n steps in their common starting point approaches 1/(2πn) for large n, which corresponds to the reciprocal of the circumference of a circle with radius n. This can show a relatively simple connection between statistics and geometry. If both BRWs start at the same time and are exactly mirrored (due to a conservation law for symmetry reasons), the probability of return is as simple as for a BRW, i.e. given by Q0(n, 0). If, on the other hand, the BRWs start later and decide seemingly independently of each other ("AND"-conjunction, (19)), the probability that they meet after n steps at the starting point k=0 is the geometric probability Q0AND(n, 0) and thus corresponds to the probability of meeting a segment of length 1 on a circle with radius n.
To get an idea of the order of magnitude in metric units, we remember that because of the slow speed of light compared to the global step frequency fmax (16), a lot can happen (1043 steps of the length smin (17) until the crossing of an atomic nucleus) until geometric (macroscopic) distances are measurable. There is always a delay to the perception of the geometric appearance, e.g., the circumference of the circle: we can then say, "The larger the macroscopic radius or distance n*smin of the circle, the more delayed is our perception of the circle, the more possibilities 2πn*smin (for positioning) on the circle there are."
Even if this reasoning starts as a two-dimensional approach at first (since a circle is a two-dimensional object), it fits the stepwise propagation of electromagnetic fields, which transport information, and in further propagation, steps include the 3rd dimension (cf. section 3.8).
Because of the uniform algorithm (3), (18) can be written analogously also for superpositions. There are further relationships, e.g.
The squares on the left side of equation (20) show no direct linear superposition. This equation holds because BRWs can be chained and because of (10) and (11). Further chaining is possible along time steps (8).
Several opportunities for further research arise. For example, equations (18) and (20) have analogies to quantum mechanical calculations of integrals and sums over squares of probability amplitudes, respectively.
3.5 Bridges to quantum mechanics: Schrödinger equation
For clarity, we assume here a non-relativistic particle in one dimension. The Schrödinger equation for this is [11]
Here Ψ(t, x) denotes the wave function or the quantum mechanical state and t and x are variables for location and time.
A function that yields a valid quantum mechanical probability amplitude as a function of location and time must also satisfy the Schrödinger equation. Therefore, the Schrödinger equation is a central tool of quantum mechanics.
However, this equation is also a differential equation on continuous sets of numbers and as such cannot be directly adopted in an information-theoretic approach. It must, in order to be compatible with 1.1, be translated into an equation with finite differences. This is indeed possible. To this end, according to (8), we identify the increase (by 1) in the number of steps n of the primary BRW (cf. Section 3.2) as the minimal condition for increase ∂t in time, and the change (by ±1) in the location coordinate k of the BRW as the minimal condition for a change ∂x in location coordinate. Application of the algorithm (3) yields
The left side of (22) represents a finite difference along the number of steps n corresponding to the derivative along the time ∂t on the left side of the Schrödinger equation (21) and the right side represents a 2nd-order finite difference along the location coordinate k corresponding to the 2nd derivative along the location coordinate ∂x on the right side of the Schrödinger equation (21).
Since the derivation (22) uses only the algorithm of the BRW (3), the same argumentation works also for all superpositions or linear combinations (5), of course also for superpositions with prefactors with opposite sign (due to physical conservation laws, see Q1-triangle, Table 2). Prefactors analogous to the Schrödinger equation are also necessary for finite differences when embedded in a larger multidimensional system. An analogy to the potential term V(t, x) in (21) becomes also necessary for finite differences (22) when embedded in a larger system. Thereby symmetries can become more apparent. For example, the potential of gravity may be a consequence of a conservation law, i.e., a global symmetry.
Validity at all superpositions can explain the universal validity of the Schrödinger equation, but ultimately also requires the synchronization of finite differences via a primary domain (cf. Section 3.7), which will be addressed in the discussion.
3.6 Bridges to quantum mechanics: (Matrix) Exponential function as binomial expansion
The complex exponential function is used as an algebraic tool in all areas of quantum mechanics. By its Taylor series expansion, we have also immediately a reference to familiar functions of geometry like sin(x) and cos(x). However, this infinite time-independent series expansion does not fit an (exact) information-theoretic approach. For this, we need an algebraic approach, whose branching depth and complexity increase discretely together with the physical time.
We have this approach in the steps of a BRW (8). The binomial coefficients (Table 1), which reflect the number of path possibilities in the BRW, can also be used to approximate the exponential function. In fact, the exponential function can be replaced by a finite binomial expansion of arbitrary precision. Let . We define:
The right-hand side of (24) corresponds to the series expansion of the exponential function. So we get
The right-hand expressions in (24) and (25) should serve as a bridge to frequently used limits of calculus and also to geometric functions because of . The binomial expansion (23) can approximate these with arbitrary accuracy, if "only" n becomes arbitrarily large. However, this can be done in a time-conformal way and thus in a reality-conformal way, if we assume that the increase of time is proportional to the sum of probabilities of return events of a BRW (8), which are proportional to binomial coefficients. Therefore, the expression (23) can better show the real combinatorics. The considerations for calculating nmax in Section 3.2 and the estimation (15) show that such reality-conforming n can become extremely large.
We initially assumed . However, this can be replaced and extended by matrices. Indeed, for illustrating important combinatorics, in particular multidimensional time-conformal combinatorics (cf. Section 3.8), matrices are more suitable than the commonly used complex numbers. In accordance with a time-conformal development starting from (), (23) can also be defined for matrices:
Here A is a square matrix and I is the unit matrix with the same dimensionality as A. Since the unit matrix I commutes with A, the series expansion (27) is uniquely defined.
The exponential function is also defined for matrices but is approximated by its Taylor series in a different order. Here it is recalled that the complex exponential function and also the matrix exponential function [12] can be replaced by a finite binomial expansion (27) and that this can provide completely new insights into the time-conformal combinatorial nature of physical processes.
It should be noted here that in the definition of the function bn(n, x) in (27), another subdivision can also be chosen, such as:
We can consider the left-hand side of (28)(29) as the decided (past) part of a BRW, and the right-hand side of (28)(29) as the undecided (future) part.
For large n, such as nmax, the right-hand sides of (28) and (29) result approximately in a symmetric distribution of the binomial coefficients as in a symmetric BRW (2). To replace the "approximately" with "exactly", there are even more combinatorial details to consider. Instead of e.g. (29) we could write for the exact consideration of a conservation law
Due to the quantization and conservation of angular momentum, it seems interesting to use for A, for example, a 3D rotation matrix (π/2 rotation about one of the 3 spatial directions, see also Table 3) and to investigate the combinatorics in more detail.
3.7 The primary domain is a prerequisite for the time-ordered exchange of energy and information and for maintaining the conservation laws
The term "primary domain" introduced above denotes the most upstream minimal common set of possibilities in this (perceptible or measurable) universe. Since a set of possibilities (domain) can only be defined under access to existing information, i.e. information from the past, the access to domains of information occurs the more frequently, the further upstream (in the past) these were defined - according to 1.1 as a selection from a (further upstream) domain. Thus, the upstream "primary domain" is maximally frequently used, but its size is minimal. It must be sufficient only for the determinability of an order.
An approach for further consideration can be given: Progressive time implies energy flow and measurable change (of information), which in turn requires access to the primary domain. The access or reference to the primary domain (ordered or "synchronized" along the progressing time) is thus a precondition for our common ordered time and necessary at every energy flow. Thus, the primary domain can be described in more detail.
For this, we examine the basics for the exchange of information between distinguishable localizations. We exchange information "outside" as free energy. Free energy "expresses" itself per proper time by an impulse to the "outside". A precise information-theoretical consideration shows that this sign of the impulse requires a synchronization along the increase of the time. This concerns the electromagnetic quanta (photons) which are our elementary information carriers. Their propagation direction decides the direction of the information transport. There is actually a decisive degree of freedom for this in the definition of the propagation vector of the energy, thus in the definition of the Poynting vector [13] Se.
Here B denotes the magnetic flux density, μ0 the field constant, and E the electric field strength. The cross product E x B defines a vector perpendicular to E and B, whose direction resp. sign depends on the order of the components E1, E2, E3 of E and B1, B2, B3 of B according to
where denote the base unit vectors of a right-handed Cartesian coordinate system and εijk denotes the Levi-Civita symbol. It is
Each of the 3 indices i, j, k represents one of the 3 orthogonal directions . How should physical systems localized at different locations immediately and reproducibly "know" (as a common past) whether the permutation of the 3 orthogonal directions is "even" or "odd"? This question is decisive for the propagation direction of the energy and therefore also decisive for all information that we exchange!
In (31) and (32) the sign of εijk determines the sign of the propagation direction of each energy exchange. This speaks for the fact that the selection of one of 2 possible orders of a common set of 3 possibilities takes place at access to the primary domain of our universe.
It is obvious that the sign of the energy flow is important to guarantee the (basic) conservation law of energy. There are further conservation laws in physics, which must be considered. For the guarantee of the conservation laws, information from the respective past must be available. How can this be stored, and how can it be guaranteed that the access can take place sufficiently fast?
One possibility is the exactly antisymmetric subsequent start of a new BRW within previously started BRWs as illustrated in Table 2 This respects the principle of "neutrality of subsequent changes" since the total sum (from the previous point of view) is preserved. This means that after each step in the primary BRW, the total sum over the conserved quantity must be equal to 0. A BRW with an antisymmetric start satisfies this condition. The example in Table 2 illustrates this; it is . According to this, the information is most quickly retrievable in the center (middle) between the starting points, i.e. in k=0 in Table 2. In k≠0 it appears as asymmetry.
We need the consequent information-theoretical approach with such pre-information for the exact synchronization at every exchange of energy. This must be guaranteed from the beginning of time. In the framework of the primary conservation law of energy, it is plausible that the global total sum of probability amplitudes over each row n is equal to 0, as in Table 2 for Q1(n, k). Then we could "simply" assume that one of the two sides k>0 or k<0 was chosen in an initial decision. This initial decision has maximum priority because starting from "rest mass" it defines the propagation direction of "energy" per time progress resp. increase in the number of steps nmax. The "probability" or access frequency in the context of a global calculation is therefore maximal. (This fits with the finding that the earlier the domain of information is learned, the faster it is available on average later).
Approaches to further research:
Since it is about the earliest decision or symmetry breaking for our universe, this could be decisive in the context of a maximum measurable symmetry. In the context of the CPT symmetry this could decide about the sign of the charge (and therefore predominance of matter over antimatter) at usual time progress resp. enlargement of the maximum number of steps.
The choice of a side e.g. k>0 and the prefactor (10) in the Q1 distribution could cause geometrical asymmetries and have further effects. It could be expressed as potential, also macroscopically, for example as gravitational potential.
3.8 Bridge to electromagnetism, Maxwell's equations, perspective
In section 3.7 we already noticed that the electromagnetic laws play a decisive role in the propagation direction of our basal information carriers resp. photons. To make these laws compatible with the basal definition of information 1.1, it is first necessary to discretize them. We start with the Maxwell Vacuum Equations with a time reference. It holds [14]
Here E denotes the electric field vector with components Ex, Ey, Ez, and B the magnetic field vector with components Bx, By, Bz, and c the speed of light, and t the time. For clarification of combinatorics, we use a notation without units. Written out in components we get from (33) with c=1:
Under suitable conditions, we can consider the expressions in the parentheses each as 2 alternatives of a BRW and thus discretize them. This becomes clearer in the form of a table (Table 3).
As with a BRW, the increase in time dt is associated with the increase in the number of steps n. The derivatives d/dx, d/dy, d/dz are linear operators. This can be transferred to the basic algorithm of the general BRW. We already noticed that the ank and bnk in (4) can be matrices or linear operators. If conditions are given that allow ordering along one dimension, a clear transfer to a BRW along one dimension k is possible as in Table 3. Different initial values lead to different further development, also with different effects of renormalization.
The alternation of dimensions in Table 3 (starting from Ez, for example, between x and y) implies that we could get closer to the combinatorics of the primary BRW (section 3.7) if we consider its steps as alternating in 2 independent directions, similar to a 2D random walk on a lattice [15]. This and further multidimensional considerations could be the subject of further research. Computer simulations could also help here, including considerations of energy propagation resp. the Poynting vector (section 3.7).
4. Discussion
The introduction first points out the need for a precise definition of information and then introduces definition 1.1, which is the focus of this article. It is mentioned that the digital application 1.2 of definition 1.1 has great potential, as this enables the systematic implementation of more and more precisely comparable and globally searchable digital information. This has been addressed in previous publications [3]. In this context, it was mentioned that the definition 1.1 also has fundamental consequences for physics.
The preparation of a physical experiment determines the set (domain) of its possible results, and the result of any physical experiment is information, i.e. a selection from the previously determined set of possibilities or domain. This just corresponds to the definition 1.1 of information. Thus, fundamental physics is actually the first science about information and should consistently apply definition 1.1 of information.
There is a lot of literature on information-theoretic approaches, also in physics. However, apart from own literature [3], there seem to be no other publications with an (exact) information-theoretic approach resulting from definition 1.1. In the last publication [3], which delves into the application of 1.1 in computer science, it has already been pointed out in Section 4.7 that the application of 1.1 in physics would also be an important topic for further research. This article is intended to provide suggestions in this regard.
The domain of information presupposed in 1.1 must always be (ordered and) reproducibly known before information exchange. That means it is finite, because after a reproducible (thus also finite) sequence of elementary steps each element of the domain must have the same meaning for all (represent identical information). Each element of the domain can only be defined with the help of information, which means selection from a previously defined domain. So we need also a discrete (and in the direction of the past even finite) concept to time and proper time.
In earlier publications [5] such a concept was already presented, starting from the relativistic time dilation, which can be represented as the sum (8) of the return probabilities of a Bernoulli Radom Walk resp. "BRW". From this, we can conclude that in the steps of a (modified, superimposed) random walk, current information and thereby the domain of later information are defined. However, this still needs to be connected (step by step) with current approaches and bridges need to be shown in particular to quantum mechanics. In connection with this, it is pointed out that also linear combinations or superpositions (5) of BRWs are possible as long as the elementary discrete steps are synchronized resp. "connected".
Since the consistent application of the elementary definition of information 1.1 (among other things because of the necessary discretization) means in the end a deep intervention into current thought buildings, the question arises whether this is necessary. Perhaps one would like to do without a clear definition of "information" because this does not fit into the present concept. Of course, nobody can be forced to do so, but this article can then clarify relevant limits and contradictions of common thought buildings and thus indirectly help to save time. We can save time, for example, if we consider the "Big Bang model" only as a way to get an overview of the first orders of magnitude (measurable here), but of course not as a starting point for the explanation of (measurable information of) reality.
Then we can also question whether we want to start the thought building at all with a clear definition of information, which is elementary (exact) and therefore starts as usual in mathematics with elementary terms of set theory. If not, what is the alternative? The experience showed again and again that the application of ill-defined or even undefined terms does not help in the end.
So the question still arises whether there is an alternative exact definition of information that differs decisively from 1.1.
The selection of elements from a set is elementary. Thereby it is quite possible to refine and extend details, especially the notion of "reproducible knowledge" (of the elements) of a set of possibilities. This requires a discrete concept of time and proper time, since "knowledge" is possible only for parts of the past. Making such a concept possible is just one of the objectives of this article.
The concept of time and proper time used here got its initial impulse from the power series development of the function (8) for relativistic time dilation. It was shown that this can be represented as the sum of the return probabilities of a Bernoulli Random Walk (BRW) [5]. The approach of a BRW allows a discrete representation of discrete sets of possibilities for information, which are always finite at a given time or a number of steps and therefore compatible with our definition of information 1.1. In Section 2 (Material and Method) it is also mentioned that the symmetric case of the BRW (p=1/2 for both sides) is particularly interesting (also for the inclusion of conservation laws). This important case occurs regularly in the ultrarelativistic case of the speed of light, i.e. the elementary electromagnetic propagation speed of information. The expression (7) results in this case in "infinity" and is therefore not usable. However, the approach to proper time via series expansion (8) as a sum of return probabilities of a symmetric BRW remains usable also in the ultrarelativistic case and shows in particular combinatorial details. The BRW approach, with additional physically relevant modifications, such as linear combinations or superpositions (e.g., Table 2) and discrete derivatives (9) of BRWs are therefore discussed in more depth and the first results are shown (Section 3).
First, a direct relationship (14) between eigentime and the number of steps of a symmetric BRW is shown. The symmetric BRW also corresponds to the "no prior information" case, since no direction is preferred. In section 3.2, this is applied to a global calculation. Consequently starting from 1.1, there must be an initially defined primary domain of information, whose knowledge is a prerequisite for any subsequent exchange of information in our universe. So to say, the "direction of time" was defined in connection with the propagation direction of energy per time increase (see section 3.7). This also means that the primary domain of information was defined in the first steps of a primary (comprehensive, thus maximum) BRW in our universe. This maximum connecting BRW is necessary for the guarantee of the conservation of energy, (cf. section 3.7) and for the synchronization of elementary finite differences (3)(4) and their possible superpositions (5).
For the sake of clarity, in section 3.2 we first made a rough estimate of the maximum number of steps nmax, since the standard deviation of the maximal BRW is and within a few standard deviations around the mean most steps of a BRW occur. Within this rough estimate, we first chose the range of the strong interaction as a measure of the standard deviation and the maximum measurable distance (i.e., the estimated extent of the measurable universe) as a measure of the extent nmax of the primary BRW. Using (15), we obtained . Rounding is more than justified because of this rough estimate. Using the range of the weak interaction would have resulted in an even larger value.
In any case, this rough estimate calculation already shows that the gradation of the discrete representation is too fine to be measurable. So it would be a fundamental mistake to conclude from missing measurability of the gradation that reality is continuous (like e.g. the "real numbers"). The information-theoretical approach 1.1 makes clear that for an information-theoretical and therefore exact description of reality we have to work from the beginning with discrete sets of numbers, which moreover have to be finite within finite time.
An exact information-theoretical approach naturally concerns quantum mechanics, where just the emphasis is put on computational models to clear basal physical experiments. Equation (18) illustrates that in the BRW approach, every progress of time can be decomposed into sums over concatenated outward and return paths. This shows first analogies to quantum mechanics, where the probability of any measurement result is the product of a probability amplitude ("outward path") with its complex conjugate probability amplitude ("return path").
Moreover, the concatenation of two BRWs leads to typical probabilities (19) of the geometric view. This shows a possibility, how in the context of further research the geometrical appearance can be derived as a statistical consequence (which occurs delayed due to limited information speed).
Section 3.5 shows a way to discretize the Schrödinger equation, here choosing the non-relativistic one-dimensional form. Despite this simplification, the analogies of derivatives of the quantum mechanical state Ψ(t, x) to discrete finite differences of Q0(n, k) shown are remarkable, since the Schrödinger equation has central importance in quantum mechanics. The algorithm of the symmetric BRW (3) is also sufficient for the argument (22). Essential is "only" the uniform definition resp. synchronization of n and k for (3) and for superposition (5). The synchronization of finite differences is necessary for the "finite" Schrödinger equation. Again, from an information-theoretic point of view, this requires the embedding of the BRWs within a maximal primary BRW with a maximal number of rows (e.g., nmax in (15)). Thus, the universal validity of the Schrödinger equation is another indication of this assumption.
The exponential function also plays an important role in quantum mechanical calculations, e.g. as part of quantum mechanical state functions. This function can be represented as a binomial expansion (23), if "only" n becomes arbitrarily large. This can be done in conformity with time [5] and thus in conformity with reality (cf. also (8)). In this case, for large n the right-hand sides of (28) and (29) show approximately a symmetric distribution of the binomial coefficients as in a symmetric BRW (2).
Section 3.7 now deals with the basal question of the minimum prior information necessary (in our universe) for elementary information exchange resp. exchange of energy quanta or photons. For this, indeed, an important degree of freedom can be found: The order of the 3 space dimensions decides the sign of the Poynting vector (30) and thus about the direction of the elementary energy transport. The fact that in (31) and (32) the sign of εijk determines the sign of the direction of propagation of any energy exchange speaks in favor of the hypothesis that the selection of one of 2 possible orders of a set of 3 possibilities takes place at access to the primary domain of our universe. We have to know this order reproducibly together as necessary pre-information at every information exchange or energy exchange (per common increase of time).
A prerequisite for this (also for the comprehensive validity of the Schrödinger equation, cf. section 3.5) is ultimately the basal discrete synchronization resp. connection of finite differences as described in (5). This and other results (sections 3.4, 3.6, 3.7) led to the title of this article.
Finally, section 3.8 describes a bridge (33) to electromagnetism. Maxwell's equations are particularly interesting because they show, with reference to time, the combinatorics of energy and information propagation in all measurable dimensions. However, for compatibility with the definition 1.1 of information, we need a discrete representation of the electromagnetic laws. Starting from the Maxwell Vacuum Equations (34)(35) written out without units, Table 3 shows the resulting combinatorics spread out along one dimension. Possibilities for further research are addressed, and multidimensional considerations and computer simulations may also be helpful.
5. Some hints for interpretation
A philosophical discussion of the definition 1.1 of information and the resulting consequences is beyond the scope of this article. However, some remarks on the interpretation are appropriate.
We are all as living beings locally separated, but ultimately part of a whole because we can exchange information, so ultimately together we must all have the same primary domain of information, which we must know more or less unconsciously. This connects all information. Access to the primary domain of information is necessary and the determined order (32) is crucial for the control of every energy flow, see section 3.7. We can consider decisions as the causes of information because we have to decide first before the information about the decision can be expressed and perceived elsewhere. The (in this reference frame or universe) primary (initial) decision defining the primary domain ("initial symmetry breaking") controls the further energy flow (per time increase) with maximum effect.
This can be done, for example, by choosing a side as shown in Table 2, i.e., by choosing one of 2 BRWs with opposite signs (because of the exact conservation law of energy - which implies that our contribution is important after all).
The initial decision defines this information with maximum effect for the further long-term common future for all life which exchanges information (as energy quanta) later.
But what does this mean for living beings, whose conscious memory usually begins much later? How shall we decide?
Since contradictory information finally extinguishes itself (due to the same primary domain and exact conservation of energy), it is certainly advisable to avoid contradictions to the common initial decision (leading into the future) and to decide to the best of our knowledge in such a way that our own decisions also lead into a common future in the long run and do not contradict the common future. To this end, we can ask ourselves:
Which decisions would future generations want from us?
6. Conclusion
Since the result of any physical, well-defined experiment is information in the form of a selection from the set of possible experimental results, definition 1.1 of information is also relevant to physics. A more detailed analysis shows that substantial consequences for theoretical physics follow from this:
The set of possibilities resp. the domain of information must be reproducibly known so that the selection from the domain (as "information") is communicable and reproducible. From this follows that within finite time the domain of information can only be finite.
Mathematical approaches to theoretical physics that use time-independent infinite sets are therefore unsuitable for an information-theoretic approach 1.1.
Starting from the series expansion of time dilation, it is shown that time is proportional to the sum of the return probabilities of a Bernoulli Random Walk or "BRW".
The BRW approach is shown to be suitable for an information theoretic approach in which the domain of information is always discrete and only increases together with time.
Starting from the BRW approach, several bridges can be formed to current mathematical approaches, e.g., to the use of linear operators, the Schrödinger equation, and the (matrix) exponential function in quantum mechanics. Bridges from BRW statistics to geometry are also possible.
The laws of electrodynamics give clues in discrete form to basic discrete combinatorics. They show 2 possibilities for the calculation of the sign of the Poynting vector (i.e. for the direction of the energy flow). From this, conclusions can be drawn to the structure of the common primary domain of information, which is necessary for the definition and connection of later defined (domains of) information. A final illustrative presentation of the combinatorics of Maxwell's equations is intended to give suggestions for further research.
- Deacon TW. What is missing from theories of information? Cambridge, UK: Cambridge University Press; 2010; 146-169.
- Floridi L. Information: A very short introduction. Oxford: OUP. 2010.
- Orthuber W. We can define the Domain of Information online and thus globally uniformly. Information. 2022; 13(5): 256.
- Korsch HJ. Mathematik der Quantenmechanik: Grundlagen, Beispiele, Aufgaben, Lösungen. München, Germany: Carl Hanser Verlag GmbH Co KG; 2019; 78-79.
- Orthuber W. A discrete and finite approach to past physical reality. International Journal of Mathematics and Mathematical Sciences. 2004; 19: 1003-1023.
- Dattoli G, Chiccoli C, Lorenzutta S, Maino G, Torre A. Theory of generalized Hermite polynomials. Computers & Mathematics with Applications. 1994; 28(4): 71-83.
- Salam A. Fundamental interaction. Access Science. 2020. doi: 10.1036/1097-8542.275600
- Bars I, Terning J, Nekoogar F. Extra dimensions in space and time. Vol. 66. New York: Springer. 2010.
- Overbye D. All the Light There Is to See? 4 x 10^84 Photons. The New York Times; 3 December 2018.
- Paris MG. The modern tools of quantum mechanics: A tutorial on quantum states, measurements, and operations. The European Physical Journal Special Topics. 2012; 203(1): 61-86.
- Schrödinger E. An undulatory theory of the mechanics of atoms and molecules. Physical Review, 1926; 28(6): 1049.
- Leonard IE. The matrix exponential. SIAM review. 1996; 38(3): 507-512.
- Richter F, Florian M, Henneberger K. Poynting's theorem and energy conservation in the propagation of light in bounded media. Europhysics Letters. 2008; 81(6): 67005.
- Maxwell JC. II. A dynamical theory of the electromagnetic field. Proceedings of the Royal Society of London; 1864; (13): 531-536.
- Caser S, Hilhorst, HJ. Topology of the support of the two-dimensional lattice random walk. Physical review letters. 1996; 77(6): 992.
Article Alerts
Subscribe to our articles alerts and stay tuned.
 This work is licensed under a Creative Commons Attribution 4.0 International License.
This work is licensed under a Creative Commons Attribution 4.0 International License.
 Help ?
Help ?

PTZ: We're glad you're here. Please click "create a new query" if you are a new visitor to our website and need further information from us.
If you are already a member of our network and need to keep track of any developments regarding a question you have already submitted, click "take me to my Query."
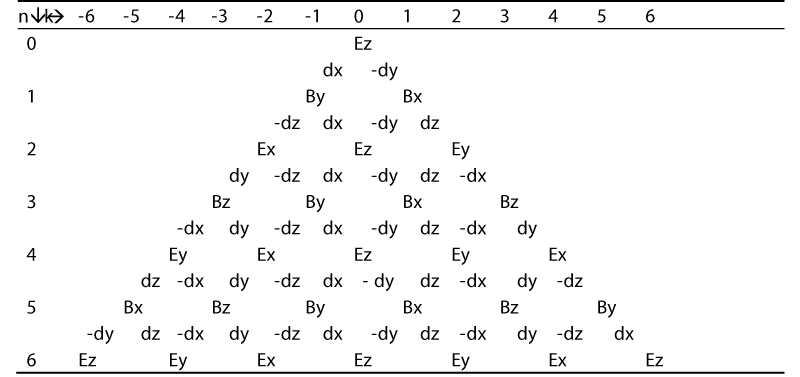


 Save to Mendeley
Save to Mendeley