Abundant dynamical solitary waves solutions of M -fractional Oskolkov model

This work uses a truncated M-fractional derivative variant of the Oskolkov model to investigate the dynamic behavior of solitary wavefronts. The methods used in this framework produce a variety of solitary waveforms, such as bright and dark solitons. A suitable choice of the free parameters is used to investigate the geometrical structures for the wave solutions, which are further characterized by stable bright periodic and soliton waves. The coefficient of the highest-order derivative and the effects of fractionality are shown in the figures. Moreover, the graphics are arranged to highlight the characteristics of novel soliton wave propagation. The findings of this research demonstrate that the fractional Oskolkov model may accommodate fundamental and higher-order soliton behaviors, each of which has unique characteristics. The fractional form of the several dynamical solitary waves seen in the study represents their practical ramifications. These waves can be seen as transmission waves via a Kelvin-Voigt fluid.

Introduction

In the present global phase of science and technology, nonlinear wave phenomena are attracting the attention of scientists and engineers more and more. For a considerable amount of time, nonlinear waves have been seen in nature, and discovering new nonlinear waves and acquiring knowledge about their basic properties are usually fascinating and challenging tasks [1-3]. Nonlinear partial differential equations (NPDEs) play a fundamental role in many scientific fields to understand nonlinear wave events, which comprise many of our daily challenges. NPDEs have garnered significant interest in the realm of nonlinear sciences owing to their diverse applications and usage throughout the last few decades. Fluid mechanics, ocean engineering, plasma physics, optical fibers, quantum physics, biology, geology, and many other scientific fields depend heavily on NPDEs to describe the dynamical, physical, and physical processes [4-8]. A relatively wide class of NPDEs has been derived to explain physical phenomena. Examples of these include the sine-Gordon equation, the Lax fifth-order KdV equation, the Korteweg-de Vries equation, the Kadomtsev-Petviashvili equation, the Sawada-Kotera equation, and many others [9-17]. In numerous scientific domains, especially in the analysis of complex nonlinear pulse phenomena, comprehending numerous physical processes is contingent upon the analytical solutions of NPDEs. In recent times, researchers have placed increasing emphasis on locating analytical solutions since these efficient computer packages facilitate the completion of difficult and time-consuming algebraic computations [18-20].

Numerous numerical and analytical solutions have emerged from various recent methodologies. These estimation techniques focus on examining the evolving wave solutions of equations, which play a crucial role in the production and develop novel computational approaches for assessing these estimated equations. Recent literature has explored diverse numerical methods for tackling linear and nonlinear PDEs. Notably, physics-informed neural networks (PINNs) have gained attention for their efficacy in solving PDEs [21]. Additionally, traditional techniques like the finite element method (FEM) remain prevalent due to their versatility in handling various types of PDEs [22-24]. A comparative study [25] evaluates the explicit finite difference method against PINNs specifically in the context of solving the Burgers' equation, shedding light on their respective strengths and limitations. This literature review highlights the evolving landscape of numerical approaches for SMITHs, emphasizing the significance of methodological comparisons to advance computational techniques in scientific research. This study presents an analytical investigation and discussion of the fractional Oskolkov model [26,27]. Therefore, it is crucial to look for wave solutions for NPDEs. To do this, scientists and researchers have devised several efficient techniques that yield precise solutions for NPDEs in a variety of forms. These methods include the Darboux transformation [28], trial solution method [29], Hirota technique [30], new Kudryashov schemes [31,32], new extended direct algebraic method [21], rational-expansion and improved Tanh scheme [33], new auxiliary method [34-37] and enhanced rational-expansion method [38] and so on.

For millennia, complex physical and biological systems have been studied through the use of fractional derivatives [38-40], a particular kind of derivative. The generalization of the ordinary derivative found in calculus is the idea of a fractional derivative in mathematics. The idea of changing the exponent of an argument of a function serves as the foundation for this definition of a derivative. Fractional derivatives provide more precise models for modeling non-linear systems and can be used to simulate second- and higher-order dynamical systems. This improves the accuracy of predictions made in domains such as signal analysis and fluid dynamics [41,42]. Recent research has examined how well fractional differential equations represent real-world issues compared to classical order. Because of this, scientists are looking for solutions to these fractional order differential equations [43,44].

Several techniques have been employed to determine the estimated analytical outcome of these so-called fractional differential equations. Within this context, we solve the M-truncated time fractional Oskolkov equation [25] using the modified auxiliary equation method (MAEM) [45,46]. The Oskolkov equation is used to determine the shape and size of a thin-walled pressure vessel, such as a tank or reactor. It is also employed in many other engineering fields, including mechanical and chemical engineering, and is particularly helpful for designing pressure vessels for applications involving high temperatures and pressures. Stress and strain, among other mechanical characteristics of a pressure vessel, can also be computed using the Oskolkov equation. The fractional Oskolkov equation has the following form

$D_{M\mathrm{,}t}^{\mu \mathrm{,}\nu }q-\varrho D_{M\mathrm{,}t}^{\mu \mathrm{,}\nu }{q}_{xx}-\vartheta q_{xx}+q{q}_x\mathrm{<mo>=</mo>0,}\text{ (1)}$

where $D_{M\mathrm{,}t}^{\mu \mathrm{,}\nu }$ is truncated M-fractional differential operator. Numerous intriguing phenomena have been made apparent by the soliton framework via the considered model M-fractional, including the possibility of localized wave packets propagating over large distances at constant speed and shape and the formation of multi-rogue waves via soliton collisions with sine-shaped functions, which explain the properties of massive type seismic waves. The governing model has never been examined using the MAEM, even though this equation has been solved previously using several analytical methods. This method has also been applied in numerous research to investigate various models. However, this method greatly simplifies the process of solving the considered model to identify new solutions. The assessment community has supported this technique from its inception due to its simple estimation process.

This article is formatted as follows: The fundamental concept of the fractional derivative is given in Section (2). In section (3), the suggested approach has been described. The governing model and the newly discovered solutions are presented in Section 4. Section 5 contains the solution solutions and a discussion of the graphical representation of the solutions. Final remarks are made in Section (6).

Fractional calculus fundamentals

A generalization of classical calculus that addresses non-integer order integration and differentiation methods is called fractional calculus. In this part, some fundamental discussions of fractional calculus are given.

M-truncated derivative

Let $\mu \mathrm{<mo>:</mo><mo\; stretchy="false">[</mo>0,}\infty \mathrm{<mo\; stretchy="false">)</mo>}\to ℝ$ then truncated-M derivative [47] of order ς is defined as

${\mathbb{F}}_{M\mathrm{,}\kappa }^{\varsigma \mathrm{,}\Omega }\mu \mathrm{<mo\; stretchy="false">(</mo>}\kappa \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\underset{{\kappa }_0\to 0}{{\displaystyle \lim }}\frac{\mu \mathrm{<mo\; stretchy="false">(</mo>}\kappa E_{\Omega }\mathrm{<mo\; stretchy="false">(</mo>}{\kappa }_0{\kappa }^{1-\varsigma }\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}-\mu \mathrm{<mo\; stretchy="false">(</mo>}\kappa \mathrm{<mo\; stretchy="false">)</mo>}}{{\kappa }_0}\mathrm{,}\mathrm{0<mo><</mo>}\varsigma \le \mathrm{1,}\gamma \mathrm{<mo>></mo>0,}$

where $E_{\Omega }\mathrm{<mo\; stretchy="false">(</mo>.<mo\; stretchy="false">)</mo>}$ is The Truncated Mittag-Leffler function of single parameter that is defined as

${}_i{E}_{\Omega }\mathrm{<mo\; stretchy="false">(</mo>}z\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{\displaystyle \sum _{k\mathrm{<mo>=</mo>0}}^i}\frac{z^k}{\Gamma \mathrm{<mo\; stretchy="false">(</mo>}\Omega k+\mathrm{1<mo\; stretchy="false">)</mo>}}\mathrm{,}$

in which Ω>0 and z∈c. Let $c_0\mathrm{,<mi>\; </mi>}{c}_1\in ℝ$ and φ and µ are ς-differentiable at a point k>0, the where co,c1 are real constants.

${\mathbb{F}}_{M\mathrm{,}\kappa }^{\varsigma \mathrm{,}\Omega }\mathrm{<mo\; stretchy="false">(</mo>}\varphi \mathrm{<mo\; stretchy="false">(</mo>}\kappa \mathrm{<mo\; stretchy="false">)</mo><mo>*</mo>}\mu \mathrm{<mo\; stretchy="false">(</mo>}\kappa \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo><mo>=</mo>}\varphi \mathrm{<mo\; stretchy="false">(</mo>}\kappa \mathrm{<mo\; stretchy="false">)</mo>}{\mathbb{F}}_{M\mathrm{,}\kappa }^{\varsigma \mathrm{,}\Omega }\mathrm{<mo\; stretchy="false">(</mo>}\mu \mathrm{<mo\; stretchy="false">(</mo>}\kappa \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}+\mu \mathrm{<mo\; stretchy="false">(</mo>}\kappa \mathrm{<mo\; stretchy="false">)</mo>}{\mathbb{F}}_{M\mathrm{,}\kappa }^{\varsigma \mathrm{,}\Omega }\mathrm{<mo\; stretchy="false">(</mo>}\varphi \mathrm{<mo\; stretchy="false">(</mo>}\kappa \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}$

${\mathbb{F}}_{M\mathrm{,}\kappa }^{\varsigma \mathrm{,}\Omega }\mathrm{<mo\; stretchy="false">(</mo>}\frac{\varphi \mathrm{<mo\; stretchy="false">(</mo>}\kappa \mathrm{<mo\; stretchy="false">)</mo>}}{\mu \mathrm{<mo\; stretchy="false">(</mo>}\kappa \mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\frac{\mu \mathrm{<mo\; stretchy="false">(</mo>}\kappa \mathrm{<mo\; stretchy="false">)</mo>}{\mathbb{F}}_{M\mathrm{,}\kappa }^{\varsigma \mathrm{,}\Omega }\mathrm{<mo\; stretchy="false">(</mo>}\varphi \mathrm{<mo\; stretchy="false">(</mo>}\kappa \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}-\varphi \mathrm{<mo\; stretchy="false">(</mo>}\kappa \mathrm{<mo\; stretchy="false">)</mo>}{\mathbb{F}}_{M\mathrm{,}\kappa }^{\varsigma \mathrm{,}\Omega }\mathrm{<mo\; stretchy="false">(</mo>}\mu \mathrm{<mo\; stretchy="false">(</mo>}\kappa \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}}{\mu {\mathrm{<mo\; stretchy="false">(</mo>}\kappa \mathrm{<mo\; stretchy="false">)</mo>}}^2}$

${\mathbb{F}}_{M\mathrm{,}\kappa }^{\varsigma \mathrm{,}\Omega }\varphi \mathrm{<mo\; stretchy="false">(</mo>}\kappa \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\frac{{\kappa }^{1-\varsigma }}{\Gamma \mathrm{<mo\; stretchy="false">(</mo>}\Omega +\mathrm{1<mo\; stretchy="false">)</mo>}}\frac{d\varphi \mathrm{<mo\; stretchy="false">(</mo>}\kappa \mathrm{<mo\; stretchy="false">)</mo>}}{d\kappa }$

${\mathbb{F}}_{M\mathrm{,}\kappa }^{\varsigma \mathrm{,}\Omega }\mathrm{<mo\; stretchy="false">(</mo>}d\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>0},\varphi \mathrm{<mo\; stretchy="false">(</mo>}\kappa \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}d$ is constant.

Description of applied method

Different analytical procedures can solve the fractional model under consideration; however, their suitability for its damping and nonlinearity may vary. This section introduces two successful analytical techniques We are going to use modified auxiliary equation method this instance.

Modified auxiliary equation scheme

According to this scheme, the solution has the following form:

$F\mathrm{<mo\; stretchy="false">(</mo>}\varsigma \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{\displaystyle \sum _{i\mathrm{<mo>=</mo>1}}^n}{r}_i{K}^{if\mathrm{<mo\; stretchy="false">(</mo>}\varsigma \mathrm{<mo\; stretchy="false">)</mo>}}+r_0+{\displaystyle \sum _{i\mathrm{<mo>=</mo>1}}^n}{\omega }_i{K}^{-if\mathrm{<mo\; stretchy="false">(</mo>}\varsigma \mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{,}\text{ (2)}$

Here ri and ωi are constants. The following auxiliary equation is satisfied by f(ς)

$f\mathrm{<mo\; stretchy="false">(</mo>}\varsigma \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\frac{1}{ln\mathrm{<mo\; stretchy="false">(</mo>}K\mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">(</mo>}a{K}^{-f}+b+\sigma K^f\mathrm{<mo\; stretchy="false">)</mo>.}\text{ (3)}$

a,b and σ are the constant to be determine later with the condition that k >0 and k≠1.

Eq. (3) has solutions in following form

Family I:

If b2-4aσ<0 and σ≠0

$K^{f\mathrm{<mo\; stretchy="false">(</mo>}\varsigma \mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{<mo>=</mo>}\frac{-b+\sqrt{4a\sigma -b^2}tan\left(\frac{\sqrt{4a\sigma -b^2}\varsigma }{2}\right)}{2\sigma }\mathrm{,}\text{ (4)}$

or

$K^f\mathrm{<mo>=</mo>}-\frac{b+\sqrt{4a\sigma -b^2}cot\left(\frac{\sqrt{4a\sigma -b^2}\varsigma }{2}\right)}{2\sigma }\mathrm{.}\text{ (5)}$

Family II:

If b²-4aσ>0 and σ≠0

$K^f\mathrm{<mo>=</mo>}-\frac{b+\sqrt{b^2-4a\sigma }tanh\left(\frac{\sqrt{b^2-4a\sigma }\varsigma }{2}\right)}{2\sigma }\mathrm{,}\text{ (6)}$

or

$K^f\mathrm{<mo>=</mo>}-\frac{b+\sqrt{b^2-4a\sigma }coth\left(\frac{\sqrt{b^2-4a\sigma }\varsigma }{2}\right)}{2\sigma }\mathrm{.}\text{ (7)}$

Family III:

If b²-4aσ=0 and σ≠0 then

$K^f\mathrm{<mo>=</mo>}-\frac{2+b\varsigma }{2\varsigma }\mathrm{.}\text{ (8)}$

Eq. (2) is inserted into the modified ODE. Based on comparing the coefficients of k^f(ς) to zero, a set of equations has been calculated. After the system is solved, the constants r0, r∈ and ω∈ are evaluated by comparing the coefficients to zero for k^f(ς). After the evaluated constants are inserted into Eq. (2), precise answers can be obtained.

Fractional governing model

Here, we use MAEM to integrate the governing model and obtain the wave solution for the fractional Oskolkov equation with a time M truncation. The model is in the following form

$D_{M\mathrm{,}t}^{\mu \mathrm{,}\nu }q-\varrho D_{M\mathrm{,}t}^{\mu \mathrm{,}\nu }{q}_{xx}-\vartheta q_{xx}+q{q}_x\mathrm{<mo>=</mo>0,}\text{ (9)}$

$\varrho$ and $\vartheta$ are parameters and q(x,t) is a wavefront. The transformation q(x,t)=G(ς) and $\varsigma \mathrm{<mo>=</mo>}k{x}^{\mu }-\lambda \frac{\Gamma \mathrm{<mo\; stretchy="false">(</mo>}\nu +\mathrm{1<mo\; stretchy="false">)</mo>}}{\mu }{t}^{\mu }$ has used to convert Eq. (9) in an ordinary differential equation (ODE). Hence, it has taken the following form:

$2k^2\lambda \varrho G^{{\text{'}}^{\prime }}-2k^2\vartheta G^{\mathrm{<mo>\text{'}</mo>}}-2\lambda G+k{G}^2\mathrm{<mo>=</mo>0,}\text{ (10)}$

where the derivative owing to is shown by G and λ be the traveling wave velocity, k be the wave number, ς be the wave variable and µ be the order of fractional derivative.

The paper's next subsection uses an analytical technique to derive the dynamical structures of wave solutions.

Novel analytical results

Applying homogeneous balance principle, it gives N=2. Taking N=2 in Eq. (2) we have solution in following form

$G\mathrm{<mo\; stretchy="false">(</mo>}\varsigma \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{r}_0+r_1{K}^{f\left(\varsigma \right)}+r_2{K}^{2f\left(\varsigma \right)}+{\omega }_1{\mathrm{<mo\; stretchy="false">(</mo>}{K}^{f\left(\varsigma \right)}\mathrm{<mo\; stretchy="false">)</mo>}}^{-1}+{\omega }_2{\mathrm{<mo\; stretchy="false">(</mo>}{K}^{f\left(\varsigma \right)}\mathrm{<mo\; stretchy="false">)</mo>}}^{-2}\mathrm{.}\text{ (11)}$

Substituting Eq. (11) into the ODE Eq. (10) and collecting terms with same power of k^f(ς) and equating to zero we get the set of algebraic equations following this set, we get the following result:

$\begin{array}{l}k\mathrm{<mo>=</mo>}-\frac{5{\omega }_1}{12a\vartheta }\mathrm{,<mi>\; </mi><mi>\; </mi><mi>\; </mi>}\lambda \mathrm{<mo>=</mo>}\frac{5\sqrt{{\omega }_1{r}_1}{\omega }_1}{6a\vartheta }\mathrm{,<mi>\; </mi><mi>\; </mi><mi>\; </mi>}\varrho \mathrm{<mo>=</mo>}-\frac{3{\vartheta }^2}{50{\omega }_1{r}_1}\mathrm{,<mi>\; </mi><mi>\; </mi><mi>\; </mi>}\sigma \mathrm{<mo>=</mo>}-\frac{r_{1}a}{{\omega }_1}\mathrm{,<mi>\; </mi><mi>\; </mi><mi>\; </mi>}{\omega }_2\mathrm{<mo>=</mo>}-\frac{\sqrt{{\omega }_1{r}_1}{\omega }_1}{4r_1}\mathrm{,}\text{ (12)}\\ r_0\mathrm{<mo>=</mo>}-\frac{3\sqrt{{\omega }_1{r}_1}}{2}\mathrm{,<mi>\; </mi><mi>\; </mi><mi>\; </mi>}{r}_2\mathrm{<mo>=</mo>}-\frac{r_1{}^2}{4\sqrt{{\omega }_1{r}_1}}\mathrm{.}\end{array}$

Utilizing the aforementioned parametric values, the solitary wave solutions of governing model can obtain as follow:

If b2-4aσ<0 and σ≠0, then

$G_1\mathrm{<mo\; stretchy="false">(</mo>}x\mathrm{,}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}-\frac{\sqrt{{\omega }_1{r}_1}{\left(\tanh \left(\frac{a\sqrt{r_1}\varsigma }{\sqrt{{\omega }_1}}\right)-1\right)}^4}{4{\left(\tanh \left(\frac{a\sqrt{r_1}\varsigma }{\sqrt{{\omega }_1}}\right)\right)}^2}\mathrm{,}\text{ (13)}$

where $\varsigma \mathrm{<mo>=</mo>}k{x}^{\mu }-\lambda \frac{\Gamma \mathrm{<mo\; stretchy="false">(</mo>}\nu +\mathrm{1<mo\; stretchy="false">)</mo>}}{\mu }{t}^{\mu }$ .

If b2-4aσ<0 and σ≠0, then

$G_2\mathrm{<mo\; stretchy="false">(</mo>}x\mathrm{,}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}-\frac{\sqrt{{\omega }_1{r}_1}{\left(\tan \left(\frac{a\sqrt{r_1}\varsigma }{\sqrt{{\omega }_1}}\right)-1\right)}^4}{4{\left(\tan \left(\frac{a\sqrt{r_1}\varsigma }{\sqrt{{\omega }_1}}\right)\right)}^2}\mathrm{,}\text{ (14)}$

where $\varsigma \mathrm{<mo>=</mo>}k{x}^{\mu }-\lambda \frac{\Gamma \mathrm{<mo\; stretchy="false">(</mo>}\nu +\mathrm{1<mo\; stretchy="false">)</mo>}}{\mu }{t}^{\mu }$ .

Graphical depiction

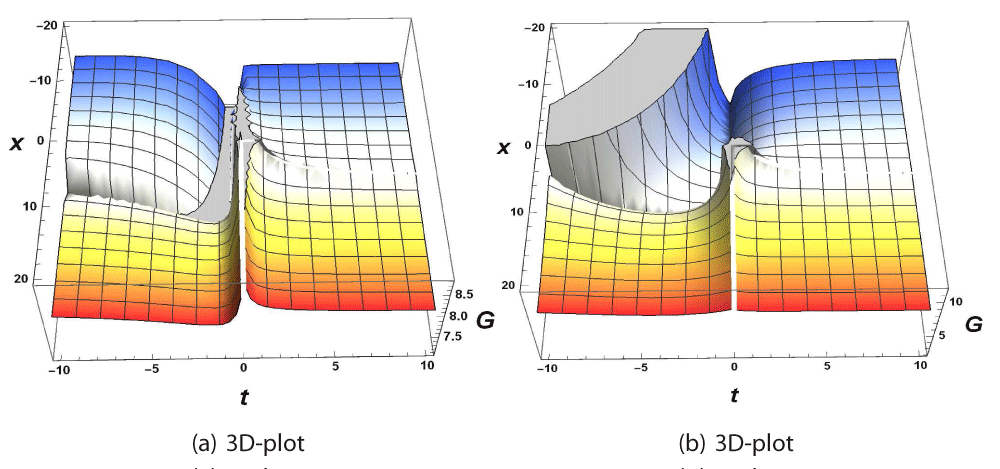
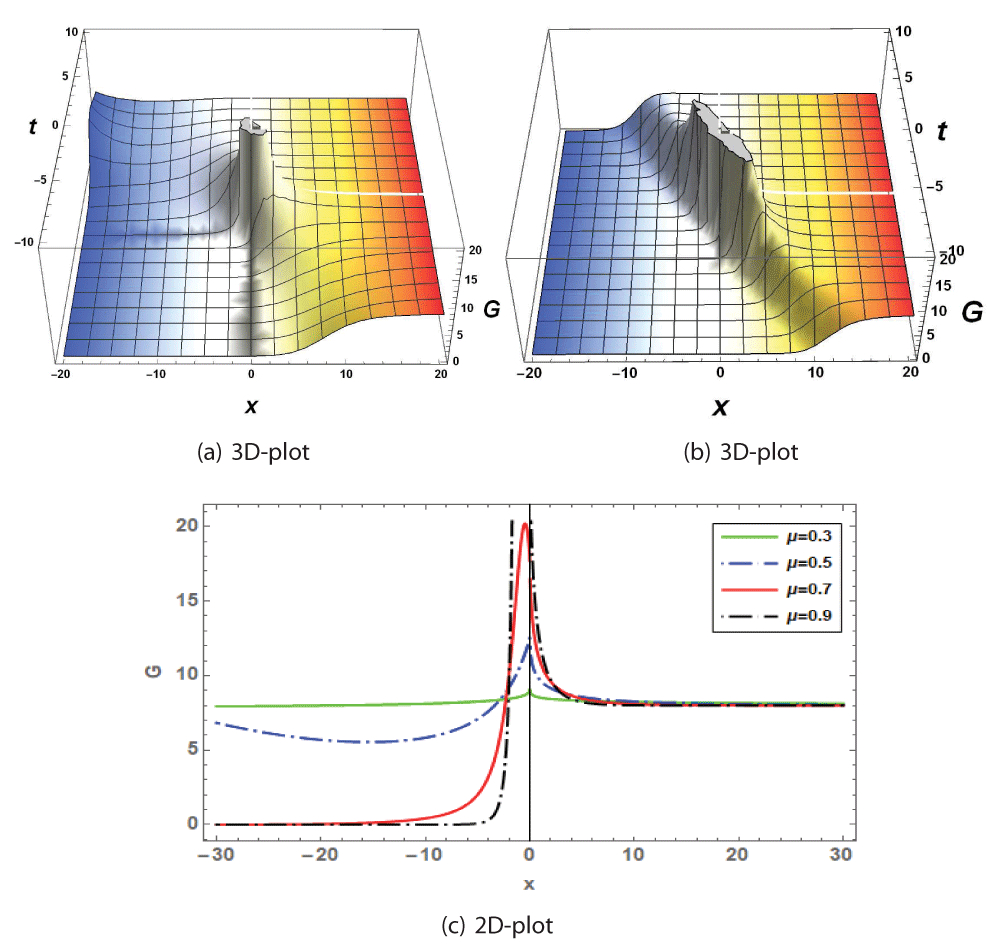
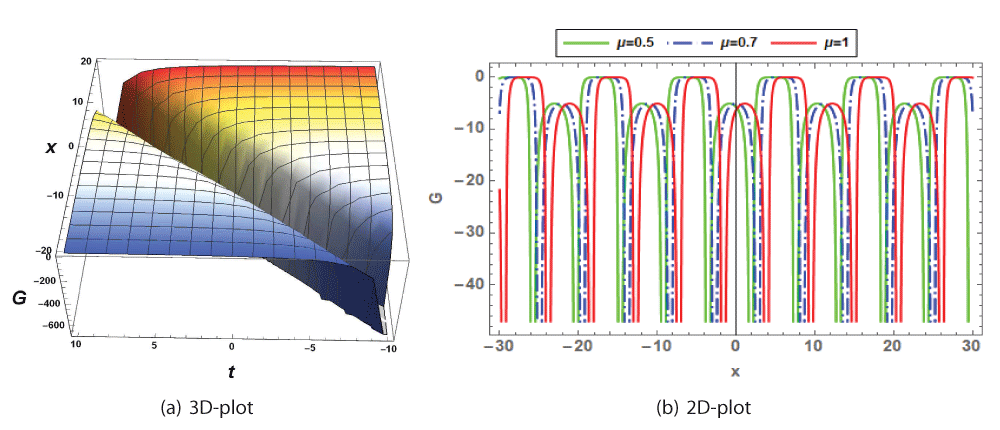
The impact of fractional parameters and the coefficient of the highest order derivative term on the 3D and 2D profiles of the identified Oskolkov model's soliton solutions are investigated in this section. Periodic, single, and dark bell solutions were investigated due to different values of the free constant. These solutions have been applied to the description of light transmission in optical fibers, water surf transmission in shallow water, and pulse propagation in a nonlinear elastic media. The acoustic impacts of dispersion and inhomogeneity on the propagation of a flow pulse can be investigated using the solitary waves of the Oskolkov model. In the figure, the effects of parameters shows with 3D as well as 2D plots. We depict the solution for Eq. (13) for , k = 0.5, λ = -0.5, v=1 and different values of as µ = 0.3, µ = 0.5 and µ = 0.7 and µ = 0.9 (Figures 1-3).

Figure 1: Graphical depiction of traveling wave solutions given in Eq. (13) µ = 0:3, and µ = 0:5.

Figure 2: Graphical depiction of traveling wave solutions given in Eq. (13) at µ = 0:7, and µ = 0:9. (a), and (b) show the 3D plot and (c) shows the combine effect of fractional parameter µ.

Figure 3: Graphical depiction of traveling wave solutions given in Eq. (14) at µ = 0:5, µ = 0:7, and µ = 1. (a) shows the 3D plot and (b) shows the combine effect of fractional parameter µ.

Conclusion

This article discusses the progress made in creating new exact soliton methods to deal with time M-fractional Oskolkov models. The nonlinear model caused by different soliton and traveling wave faces is solved using the modified auxiliary equation method. In fact, using this technique, we were able to get fractional-time solutions that were stated as rational functions and polynomial functions with a few free parameters. The computations led to some creative exact solutions for the unique value of the free parameters. Figures 1 through 3 show these solutions together with matching three-, and two-dimensional graphs. Furthermore, by using the differentiation parameters µ as 1, 0.7, and 0.5 in the preceding picture, we were able to effectively illustrate the impacts of truncated M-fractionally. The findings thus demonstrate that projected scheme is highly successful, straightforward, and efficient in comprehending the nature of waves, and that solutions from the Oskolkov model represent more authentic natural events than those derived from alternative techniques.

1. Rahman RU, Riaz MB, Martinovic J, Tunç O. Exploring analytical solutions and modulation instability for the nonlinear fractional Gilson-Pickering equation. Results in Physics. 2024;107385.
2. Az-Zo'bi EA, Afef K, Ur Rahman R, Akinyemi L, Bekir A, Ahmad H, Tashtoush MA, Mahariq I. Novel topological, non-topological, and more solitons of the generalized cubic p-system describing isothermal flux. Optical and Quantum Electronics. 2024; 56(1):84.
3. Kivshar YS, Malomed BA. Dynamics of solitons in nearly integrable systems. Reviews of Modern Physics. 1989; 61(4):763.
4. Rahman RU, Hammouch Z, Alsubaie AS, Mahmoud KH, Alshehri A, Az-Zo'bi EA, Osman MS. Dynamical behavior of fractional nonlinear dispersive equation in Murnaghan's rod materials. Results in Physics. 2024; 56:107207.
5. Abbott BP, Abbott R, Abbott TD, Abernathy MR, Acernese F, et al. GW151226: Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence. Phys Rev Lett. 2016 Jun 17;116(24):241103. doi: 10.1103/PhysRevLett.116.241103. Epub 2016 Jun 15. PMID: 27367379.
6. Ablowitz MJ, Zeppetella A. Explicit solutions of Fisher's equation for a special wave speed. Bulletin of Mathematical Biology. 1979; 41(6):835-40.
7. Rahman RU, Qousini MM, Alshehri A, Eldin SM, El-Rashidy K, Osman MS. Evaluation of the performance of fractional evolution equations based on fractional operators and sensitivity assessment. Results in Physics. 2023; 49:106537.
8. Rahman RU, Raza N, Jhangeer A, Inc M. Analysis of analytical solutions of fractional Date-Jimbo-Kashiwara-Miwa equation. Physics Letters A. 2023; 470:128773.
9. Gürses M, Pekcan A. Nonlocal nonlinear Schrödinger equations and their soliton solutions. Journal of Mathematical Physics. 2018; 59(5).
10. Triki H, Ak T, Moshokoa S, Biswas A. Soliton solutions to KdV equation with spatio-temporal dispersion. Ocean Engineering. 2016; 114:192-203.
11. Chakravarty S, Kodama Y. Soliton solutions of the KP equation and application to shallow water waves. Studies in Applied Mathematics. 2009; 123(1):83-151.
12. Oad A, Arshad M, Shoaib M, Lu D, Li X. Novel soliton solutions of two-mode sawada-kotera equation and its applications. IEEE Access. 2021; 9:127368-81.
13. Akbar MA, Akinyemi L, Yao SW, Jhangeer A, Rezazadeh H, Khater MM, Ahmad H, Inc M. Soliton solutions to the Boussinesq equation through sine-Gordon method and Kudryashov method. Results in Physics. 2021; 25:104228.
14. Wazwaz AM. The extended tanh method for new solitons solutions for many forms of the fifth-order KdV equations. Applied Mathematics and Computation. 2007; 184(2):1002-14.
15. Ur Rahman R, Faridi WA, El-Rahman MA, Taishiyeva A, Myrzakulov R, Az-Zo'bi EA. The sensitive visualization and generalized fractional solitons construction for regularized long-wave governing model. Fractal and Fractional. 2023; 7(2):136.
16. Rahman RU, Al-Maaitah AF, Qousini M, Az-Zo'bi EA, Eldin SM, Abuzar M. New soliton solutions and modulation instability analysis of fractional Huxley equation. Results in Physics. 2023; 44:106163.
17. Haroon S, Abuzar M, Khan MF. Analyzing sensitivity and solitonic behavior using the Dullin-Gottwald-Holm model in shallow water waves. Acadlore Trans. Appl Math. Stat. 2023; 1(2):96-110.
18. Eidinejad Z, Saadati R, Li C, Inc M, Vahidi J. The multiple exp-function method to obtain soliton solutions of the conformable Date-Jimbo-Kashiwara-Miwa equations. International Journal of Modern Physics B. 2024; 38(03):2450043.
19. Gu Q, Li S, Liao Z. Solving nonlinear equation systems based on evolutionary multitasking with neighborhood-based speciation differential evolution. Expert Systems with Applications. 2024; 238:122025.
20. Ahmad J, Akram S, Ali A. Analysis of new soliton type solutions to generalized extended (2+1)-dimensional Kadomtsev-Petviashvili equation via two techniques. Ain Shams Engineering Journal. 2024; 15(1):102302.
21. Ahmad H, Qousini M, Rahman RU. An enormous diversity of fractional-soliton solutions with sensitive prodigy to the TZItzeica-Dodd-Bullough equation. Optical and Quantum Electronics. 2024; 56(5):1-22.
22. Raissi M, Perdikaris P, Karniadakis GE. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational physics. 2019; 378:686-707.
23. Zienkiewicz OC, Taylor RL, Zhu JZ. The finite element method: its basis and fundamentals. 2005. Elsevier.
24. Hughes TJ. The finite element method: linear static and dynamic finite element analysis. Courier Corporation. 2012.
25. Savovic S, Ivanovic M, Min R. A Comparative Study of the Explicit Finite Difference Method and Physics-Informed Neural Networks for Solving the Burgers' Equation. Axioms. 2023; 12(10):982.
26. Roshid M, Abdeljabbar A, Begum M, Basher H. Abundant dynamical solitary waves through Kelvin-Voigt fluid via the truncated M-fractional Oskolkov model. Results in Physics. 2023; 55:107128.
27. Thabet H, Kendre S, Peters J. Advances in solving conformable nonlinear partial differential equations and new exact wave solutions for Oskolkov-type equations. Mathematical Methods in the Applied Sciences. 2022; 45(5):2658-73.
28. Matveev VB, Salle MA. Darboux transformations and solitons. Berlin: Springer; 1991.
29. Biswas A, Mirzazadeh M, Eslami M, Zhou Q, Bhrawy A, Belic M. Optical solitons in nano-fibers with spatio-temporal dispersion by trial solution method. Optik. 2016; 127(18):7250-7.
30. Zhou Y, Ma WX. Complexiton solutions to soliton equations by the Hirota method. Journal of Mathematical Physics. 2017; 58(10).
31. Raza N, Ur Rahman R, Seadawy A, Jhangeer A. Computational and bright soliton solutions and sensitivity behavior of Camassa-Holm and nonlinear Schrödinger dynamical equation. International Journal of Modern Physics B. 2021; 35(11):2150157.
32. Zayed EM, Shohib RM, Alngar ME. New extended generalized Kudryashov method for solving three nonlinear partial differential equations. Nonlinear Analysis: Modelling and Control. 2020; 25(4):598-617.
33. Seadawy AR, El-Rashidy K. Application of the extension exponential rational function method for higher-dimensional Broer-kaup-Kupershmidt dynamical system. Modern Physics Letters A. 2020; 35(01):1950345.
34. Hassan Z, Raza N, Abdel-Aty AH, Zakarya M, Rahman RU, Yasmeen A, Muse AH, Mahmoud EE. New fractal soliton solutions and sensitivity visualization for double-chain DNA model. Journal of Function Spaces. 2022.
35. Riaz MB, Wojciechowski A, Oros GI, Rahman RU. Soliton Solutions and Sensitive Analysis of Modified Equal-Width Equation Using Fractional Operators. Symmetry. 2022; 14(8):1731.
36. Jhangeer A, Almusawa H, Rahman RU. Fractional derivative-based performance analysis to Caudrey-Dodd-Gibbon-Sawada-Kotera equation. Results in Physics. 2022; 36:105356.
37. Raza N, Hassan Z, Butt AR, Rahman RU, Abdel-Aty AH, Mahmoud M. New and more dual-mode solitary wave solutions for the Kraenkel-Manna-Merle system incorporating fractal effects. Mathematical Methods in the Applied Sciences. 2022; 45(5):2964-83.
38. Veeresha P, Prakasha DG, Kumar S. A fractional model for propagation of classical optical solitons by using nonsingular derivative. Mathematical Methods in the Applied Sciences. 2020.
39. Raza N, Jhangeer A, Rahman RU, Butt AR, Chu YM. Sensitive visualization of the fractional Wazwaz-Benjamin-Bona-Mahony equation with fractional derivatives: A comparative analysis. Results in Physics. 2021; 25:104171.
40. Arshed S, Raza N, Rahman RU, Butt AR, Huang WH. Sensitive behavior and optical solitons of complex fractional Ginzburg-Landau equation: A comparative paradigm. Results in Physics. 2021; 28:104533.
41. Az-Zo'bi EA, AlZoubi WA, Akinyemi L, Senol M, Alsaraireh IW, Mamat M. Abundant closed-form solitons for time-fractional integro-differential equation in fluid dynamics. Optical and Quantum Electronics. 2021; 53:1-6.
42. Singer AC, Oppenheim AV, Wornelly GW. Detection and estimation of multiplexed soliton signals. IEEE Transactions on Signal Processing. 1997; 45(8):2146.
43. Arshed S, Rahman RU, Raza N, Khan AK, Inc M. A variety of fractional soliton solutions for three important coupled models arising in mathematical physics. International Journal of Modern Physics B. 2022; 36(01):2250002.
44. Ablowitz MJ, Been JB, Carr LD. Fractional Integrable Nonlinear Soliton Equations. Phys Rev Lett. 2022 May 6;128(18):184101. doi: 10.1103/PhysRevLett.128.184101. PMID: 35594099.
45. Khater M, Lu D, Attia RA. Dispersive long wave of nonlinear fractional Wu-Zhang system via a modified auxiliary equation method. AIP Advances. 2019; 9(2).
46. Khater MM, Attia RA, Lu D. Modified auxiliary equation method versus three nonlinear fractional biological models in present explicit wave solutions. Mathematical and Computational Applications. 2018; 24(1):1.
47. Yusuf A, In M, Baleanu D. Optical solitons with M-truncated and beta derivatives in nonlinear optics. Frontiers in Physics. 2019; 7:126.