Analyzing Riemann's hypothesis

In this paper we perform a detailed analysis of Riemann's hypothesis, dealing with the zeros of the analytically-extended zeta function. We use the functional equation $\zeta (s)=2^s{\pi }^{s-1}sin(\pi s/2)\Gamma (1-s)\zeta (1-s)$ for complex numbers s such that 0< Re(s)< 1, and the reduction to the absurd method, where we use an analytical study based on a complex function and its modulus as a real function of two real variables, in combination with a deep numerical analysis, to show that the real part of the non-trivial zeros of the Riemann zeta function is equal to ½, to the best of our resources. This is done in two steps. First, we show what would happen if we assumed that the real part of s has a value between 0 and 1 but different from 1/2, arriving at a possible contradiction for the zeros. Second, assuming that there is no real value y such that ζ(1/2+yi)=0, by applying the rules of logic to negate a quantifier and the corresponding Morgan's law we also arrive at a plausible contradiction. Finally, we analyze what conditions should be satisfied by y∈ℝ such that ζ(1/2+yi)=0. While these results are valid to the best of our numerical calculations, we do not observe and foresee any tendency for a change. Our findings open the way towards assessing the validity of Riemman's hypothesis from a fresh and new mathematical perspective.

Introduction

Riemann's hypothesis, first formulated by Bernhard Riemann in 1859 [1], is a conjecture about the distribution of the zeros of the Riemann zeta function ζ(s) [2]. Due to its relationship with the distribution of prime numbers in the set of natural numbers, proving this hypothesis is one of the most important open problems in contemporary mathematics [3,4].

In this paper, we analyze Riemman's hypothesis by dealing with the zeros of the analytically-extended zeta function. To be specific, we make use of the functional equation $\zeta {\text{(s)=2}}^{\text{s}}{\text{π}}^{\text{s-1}}\text{sin(πs/2)}\Gamma \text{(1-s)}\zeta \text{(1-s)}$ for complex numbers s such that 0< Re(s)< 1. Our goal is to assess if it can really be true that the only non-trivial zeros of the Riemann zeta function are those complex numbers whose real part is equal to 1/2. We pursue this analysis using a combination of analytical and numerical techniques, as discussed in detail below.

Previous research

Riemann's hypothesis is also the central subject of a lot of recent research. For instance, establishing an analogue to Lagaria's criterion for the hypothesis in terms of harmonic series [5]. Describing the connection between the zeta function and the solution of the Majorana fermionic equation in curved space-times [6]. Studies on the validity of the hypothesis via statistical analysis of the Mertens function [7]. In addition, making use of Riemann's hypothesis to obtain asymptotic formulas for the second moment of the nth antiderivative of the argument of the zeta function [8]. Studies of ergodic theorems to provide new characterisations of the hypothesis [9]. It was observed that the zeta function corresponds to the spectrum of a certain quantum Hamiltonian capturing the near-horizon dynamics of the Schwarzschild black hole [10]. Works that describe an algorithm to compute very high Riemann zeros using random walks [11]. Another work provides a Riesz-type criterion for the generalized Riemann hypothesis [12]. It was considered an analogue of the hypothesis and quantum walks [13]. A Riesz-type criterion for the hypothesis in terms of one variable was also provided in [14]. Deformations of the Keiper-Li sequence were considered to analyze the hypothesis [15]. A positivity conjecture was proposed for matrices related directly to the hypothesis [16]. Studies on the meromorphic extensions of fractal zeta function from quasiperiodic sets [17]. Also regarding meromorphic functions, [18] it was considered the meromorphic modular forms of a family of generalized L-functions and relates them to the zeta function.

Additionally, other important research works were published recently that have a connection to our work. An example is the new results by Conrey [19], who analyzes that the major difficulty when trying to prove the hypothesis through analysis comes from the fact that the zeros of L-functions have a very different behavior to the zeros of many of the special mathematical functions, and only recently it was found that the modularity of the L-functions is associated to elliptic curves, which could help in this direction. Moreover, recent work by Liu [20] attempts to prove the Riemann hypothesis for both the Riemann zeta-function ζ(s) and the Dirichlet L-function L(s,x) through an equivalent condition on the Farey series set forth by Franel and Landau. Finally, Liu and Wang analyzed recently [21] the Riemann problem of the high-order Jaulent-Miodek (JM) equation with initial data of step discontinuity, as explored by Whitham modulation theory, and found that the periodic wave solutions of the high-order JM equation are described by the elliptic function along with the Whitham modulation equations.

The hypothesis has also been the subject of intensive research works in the past in several ambits, see for instance [22-31] and references therein.

Daily-life applications

Even if belonging to the field of pure mathematics, this hypothesis also has applications in our daily life. We have already mentioned some of them above when enumerating references to previous important and recent research works. To put everything in context, let us discuss briefly some of these applications here. The hypothesis also finds a wide spectrum of applications in science and technology. For instance, the zeros of the zeta function have important connections to the energy spectrum of classical chaotic systems [32], quantum Hamiltonians [33], as well as to scattering amplitudes in quantum field theory [34]. Quantum physics is currently around us, and future computers, not so far in time, will process information directly at a quantum level. The hypothesis has therefore a direct impact on the upcoming quantum technologies and their industrial implications [35]. In addition, there are also important implications in the field of cryptography. The zeros of the zeta function can be interpreted as harmonic frequencies in the distribution of primes, leading to studies of the distribution of distances between consecutive primes [36]. Such analysis is key in the security of asymmetric-key cryptosystems such as RSA, which is based on the fact that finding the prime factorization of a natural number is a hard computational problem [37], though not for quantum computers [38]. Though RSA is no longer used as a standard cryptographic protocol (in favor of symmetric-key schemes), it has been a technical standard for many years and still, as of today, is used in certain non-critical applications. There are many other daily-life applications of the hypothesis. Apart from encryption algorithms, which rely heavily on the properties of prime number distributions, zeros of the zeta function are also related to particle distributions in quantum statistical mechanics, as well as to the eigenvalues of random matrices [39]. As such, random matrices have by themselves a very wide spectrum of practical applications, including the energies of heavy uranium-like nuclei, the behaviour and dynamics of financial markets, and even the development of new machine learning and Artificial Intelligence (AI) algorithms based on neural networks and deep learning. And this last point is intriguing since new techniques are required to boost performance and decrease the energy consumption of current AI models, such as Large Language Models [40]. In this overall context, the hypothesis also impacts the currently advanced software used for cybersecurity and artificial intelligence, such as the EC3 Software [41].

About this paper

As said above, here we analyze Riemman's hypothesis by dealing with the zeros of the analytically-extended zeta function using the functional equation $\zeta (s)=2^s{\pi }^{s-1}sin(\pi s/2)\Gamma (1-s)\zeta (1-s)$ for complex numbers s such that 0< Re(s)< 1. The objective of this analysis is to show if it can really be true that the only non-trivial zeros of the Riemann zeta function, using its functional equation, are those complex numbers whose real part is equal to 1/2. More specifically, we want to show that if x is a real number such that 0<x<1, then it can be satisfied that there exists y∈ℝ such that ζ(x+iy) = 0 if and only if x = 1/2. In order to develop our analysis, we will use a combination of two mathematical methods. The first method is an analytical technique called reduction to the absurd, and the second one is based on numerical analysis techniques using two different types of specialized mathematical software: Matlab and Wolfram Alpha. The reduction to the absurd method is a very usual and well-known technique, when we want to prove that a conditional statement such as ``If A happens, then B happens" is true. As we shall see, in this paper, we make use that, if the statement ``If A happens, then B happens" is true, then by using the fundamental laws of mathematical logic, the negated statement must also be true. That is, ``If B does not happen, then A does not happen" must also be true. In this way, here we will usually that ``A happens" but ``B does not happen". In this way if we are able to show that ``A does not happen", then we arrive at what we call a contradiction because we were assuming that ``A happens". And, therefore, the statement ``If B does not happen, then A does not happen" is true, and ``If A happens, then B happens" is also true. Additionally, the numerical analysis method is based on algorithms developed using Matlab and Wolfram Alpha. Note that, like all techniques based on numerical analysis, in our algorithms, some of the calculations will be iterated until a sufficiently small error is attained, which we take as convergence criteria. In our numerical approach, both Matlab and Wolfram Alpha work up to a preset error given by machine precision. Therefore, of course, the numerical analysis methods work under certain assumptions, like not exceeding a certain accepted (minimum and small enough) error, as well as other limitations coming from potential sources of error such as floating point errors. As for specific algorithms, in Matlab, we will use the ``gradient-free Nelder-Mead algorithm" to minimize two functions to the best of our numerical capabilities. And Wolfram Alpha is used to solve a non-linear system of equations. See Appendix A for more detailed information on our numerical methods. Diving into more details of our actual derivations, as a first step, we show two Propositions that we use later to work analytically throughout the whole paper.

Using the reduction to the absurd method, we develop an analytical study based on a complex function, and its modulus as a real function of two real variables. And at a certain point in our study, we combine it with intensive numerical analysis at some steps. Our derivations are compatible with the real part of the non-trivial zeros of the Riemann zeta function being equal to 1/2, to the best of our resources.

We do this in two steps. First, we show what would happen if we assume that the real part of s has a value between 0 and 1 but different from 1/2, arriving at a possible contradiction for the zeros. Second, assuming that there is no real value y such that ζ(1/2+yi)=0, and by applying the rules of logic to negate a quantifier together with the corresponding Morgan's law, we also arrive at a plausible contradiction.

Finally, we also analyze what conditions should be satisfied by y∈ℝ such that ζ(1/2+yi)=0. While most of our results are fully analytic, at some specific parts of the analysis we need to rely on heavy numerical calculations. Some part of our analysis is therefore dependent on them. However, we do not observe nor foresee any tendency for a change in our calculations, which leads us to conjecture that the validity of our conclusions is general. Our approach also opens the way toward a new mathematical angle to assess Riemman's hypothesis.

The paper is organized as follows. In Sec.2 we review the basics of the hypothesis. In Sec.3 we implement our analysis, as briefly outlined above. In Sec.4 we provide analytical constraints to be satisfied by the zeros that come out naturally from our analysis. Finally, in Sec.5 we wrap up our conclusions and perspectives for future work. In addition, in Appendix A we provide the Matlab computer codes used and give a brief explanation of the numerical techniques used both with Matlab and with Wolfram Alpha.

Zeta function and Riemman's hypothesis

The Riemann zeta function ζ(s) is defined in complex numbers as the sum of an infinite series as follows:

$\zeta \mathrm{<mo\; stretchy="false">(</mo>}s\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{\displaystyle \sum _{n\mathrm{<mo>=</mo>1}}^{\infty }}\frac{1}{n^s}\mathrm{.}\text{ (1)}$

The series is convergent when Re(s) is strictly greater than 1. Leonhard Euler showed that this series is equivalent to Euler's product,

$\zeta \mathrm{<mo\; stretchy="false">(</mo>}s\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{\displaystyle \prod _{p\text{p}rime}}\frac{1}{1-p^{-s}}\mathrm{,}\text{ (2)}$

Where the infinite product extends over the set of all prime numbers p and again converges for a complex s whose real part is greater than 1. The convergence of the Euler product shows that ζ(s) has no zeros in this region since none of the factors in the product have zeros.

Riemann's hypothesis deals with the zeros outside the convergence radius of the series in Eq.(1) and/or the Euler product in Eq.(2). To preserve the meaning of this hypothesis, one needs to analytically continue the zeta function ζ(s), so that it makes sense for any value of s. Any choice of extension will lead to the same conclusions as above since the zeta function is meromorphic. Hence, in particular, for complex numbers s such that 0< Re(s)< 1, the function ζ(s) can be expressed by the functional equation

$\zeta (s)=2^s{\pi }^{s-1}\sin \left(\frac{\pi s}{2}\right)\Gamma \mathrm{<mo\; stretchy="false">(</mo>1}-s\mathrm{<mo\; stretchy="false">)</mo>}\zeta \mathrm{<mo\; stretchy="false">(</mo>1}-s\mathrm{<mo\; stretchy="false">)</mo>,}\text{ (3)}$

Where Г(s) is the Gamma function, defined by

$\Gamma \mathrm{<mo\; stretchy="false">(</mo>}s\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{\displaystyle {\int }_0^{\infty }}{t}^{s-1}{e}^{-t}dt\mathrm{.}\text{ (4)}$

In this work, we will make extensive use of this functional form.

From now on, we consider the zeros of the above analytical extension of the zeta function. Some of these zeros are called "trivial" since they can be easily seen by inspection. In particular, from Eq.(3) one can see that s =-2,-4,-6,…, i.e., all negative even integers, are trivial zeros since they cancel the trigonometric function. Likewise, there are other (complex) values of s such that 0< Re(s)< 1 and for which the zeta function also vanishes, which are called "non-trivial" zeros. The Riemann conjecture refers specifically to these non-trivial zeros, stating the following:

The real part of all non-trivial zeros of the Riemann zeta function is equal to 1/2.

The conjecture, therefore, implies that all the non-trivial zeros should lie on the critical line s= ½+it, where t is a real number and i is the imaginary unit.

Analysis of the hypothesis

Let us start our analysis with the following two propositions

Proposition 1: Using Riemann's zeta functional equation, it is satisfied that, Ɐs∈ℂ such that 0< Re(s)< 1 and ζ(s) = 0, then ζ(1-s) = 0.

Proof: Given Riemann's zeta functional equation in Eq.(3), then ζ(1-s) is equal to

$\zeta (1-s)=2^{1-s}{\pi }^{-s}\sin \left(\frac{\pi \mathrm{<mo\; stretchy="false">(</mo>1}-s\mathrm{<mo\; stretchy="false">)</mo>}}{2}\right)\Gamma \mathrm{<mo\; stretchy="false">(</mo>}s\mathrm{<mo\; stretchy="false">)</mo>.}\zeta \mathrm{<mo\; stretchy="false">(</mo>}s\mathrm{<mo\; stretchy="false">)</mo>.}\text{ (5)}$

Therefore, if there exists an s∈ℂ such that 0< Re(s)< 1 and ζ(s)=0, then by the previous equation we have that

$\zeta (1-s)=2^{1-s}{\pi }^{-s}\sin \left(\frac{\pi \mathrm{<mo\; stretchy="false">(</mo>1}-s\mathrm{<mo\; stretchy="false">)</mo>}}{2}\right)\Gamma \mathrm{<mo\; stretchy="false">(</mo>}s\mathrm{<mo\; stretchy="false">)</mo>}\cdot \mathrm{0<mo>=</mo>0,}\text{ (6)}$

which proves the proposition.

Proposition 2: It is satisfied that $\zeta \mathrm{<mo\; stretchy="false">(</mo>}a-bi\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\overline{\zeta \mathrm{<mo\; stretchy="false">(</mo>}a+bi\mathrm{<mo\; stretchy="false">)</mo>}}$ .

Proof: Using the definition of ζ(a+bi), we have that

$\zeta \mathrm{<mo\; stretchy="false">(</mo>}a+bi\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{\displaystyle \sum _{n\mathrm{<mo>=</mo>1}}^{\infty }}\frac{1}{n^{a+bi}}\mathrm{.}\text{ (7)}$

This implies that

$\zeta \mathrm{<mo\; stretchy="false">(</mo>}a+bi\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{\displaystyle \sum _{n\mathrm{<mo>=</mo>1}}^{\infty }}\frac{n^{-bi}}{n^a}\mathrm{<mo>=</mo>}{\displaystyle \sum _{n\mathrm{<mo>=</mo>1}}^{\infty }}\frac{e^{\ln \mathrm{<mo\; stretchy="false">(</mo>}{n}^{-bi}\mathrm{<mo\; stretchy="false">)</mo>}}}{n^a}\mathrm{,}$

$\mathrm{<mo>=</mo>}{\displaystyle \sum _{n\mathrm{<mo>=</mo>1}}^{\infty }}\frac{e^{-ib\ln \mathrm{<mo\; stretchy="false">(</mo>}n\mathrm{<mo\; stretchy="false">)</mo>}}}{n^a}\mathrm{<mo>=</mo>}{\displaystyle \sum _{n\mathrm{<mo>=</mo>1}}^{\infty }}\frac{\cos \mathrm{<mo\; stretchy="false">(</mo>}b\ln \mathrm{<mo\; stretchy="false">(</mo>}n\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}-i\sin \mathrm{<mo\; stretchy="false">(</mo>}b\ln \mathrm{<mo\; stretchy="false">(</mo>}n\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}}{n^a}\mathrm{,}$

$\mathrm{<mo>=</mo>}{\displaystyle \sum _{n\mathrm{<mo>=</mo>1}}^{\infty }}\frac{\cos \mathrm{<mo\; stretchy="false">(</mo>}b\ln \mathrm{<mo\; stretchy="false">(</mo>}n\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}}{n^a}-i{\displaystyle \sum _{n\mathrm{<mo>=</mo>1}}^{\infty }}\frac{\sin \mathrm{<mo\; stretchy="false">(</mo>}b\ln \mathrm{<mo\; stretchy="false">(</mo>}n\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}}{n^a}\mathrm{.}\text{ (8)}$

If we do the same but for ζ(a-bi), we have that

$\zeta \mathrm{<mo\; stretchy="false">(</mo>}a-bi\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{\displaystyle \sum _{n\mathrm{<mo>=</mo>1}}^{\infty }}\frac{n^{bi}}{n^a}\mathrm{<mo>=</mo>}{\displaystyle \sum _{n\mathrm{<mo>=</mo>1}}^{\infty }}\frac{e^{\ln \mathrm{<mo\; stretchy="false">(</mo>}{n}^{bi}\mathrm{<mo\; stretchy="false">)</mo>}}}{n^a}\mathrm{,}$

$\mathrm{<mo>=</mo>}{\displaystyle \sum _{n\mathrm{<mo>=</mo>1}}^{\infty }}\frac{e^{ib\ln \mathrm{<mo\; stretchy="false">(</mo>}n\mathrm{<mo\; stretchy="false">)</mo>}}}{n^a}\mathrm{<mo>=</mo>}{\displaystyle \sum _{n\mathrm{<mo>=</mo>1}}^{\infty }}\frac{\cos \mathrm{<mo\; stretchy="false">(</mo>}b\ln \mathrm{<mo\; stretchy="false">(</mo>}n\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}+i\sin \mathrm{<mo\; stretchy="false">(</mo>}b\ln \mathrm{<mo\; stretchy="false">(</mo>}n\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}}{n^a}\mathrm{,}$

$\mathrm{<mo>=</mo>}{\displaystyle \sum _{n\mathrm{<mo>=</mo>1}}^{\infty }}\frac{\cos \mathrm{<mo\; stretchy="false">(</mo>}b\ln \mathrm{<mo\; stretchy="false">(</mo>}n\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}}{n^a}+i{\displaystyle \sum _{n\mathrm{<mo>=</mo>1}}^{\infty }}\frac{\sin \mathrm{<mo\; stretchy="false">(</mo>}b\ln \mathrm{<mo\; stretchy="false">(</mo>}n\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}}{n^a}\mathrm{.}\text{ (9)}$

Therefore, comparing the above equations, we see that $\zeta \mathrm{<mo\; stretchy="false">(</mo>}a-bi\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\overline{\zeta \mathrm{<mo\; stretchy="false">(</mo>}a+bi\mathrm{<mo\; stretchy="false">)</mo>}}$ , as we want to prove.

We now dive into the actual details of Riemann's conjecture. As a reminder, this reads as follows:

Riemann hypothesis: Let x be a real number such that $0<x<1$ . Then, it is satisfied that $\exists y\in ℝ$ such that $\zeta (x+yi)=0$ if and only if $x\mathrm{<mo>=</mo>1<mo>/</mo>2}$ .

Our approach to the conjecture is as follows. Let x be a real number such that 0< x< 1. We assess the validity of the double implication and start with the first direction.

i. If $\exists y\in ℝ$ such that $\zeta \mathrm{<mo\; stretchy="false">(</mo>}x+yi\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>0}$ then $x\mathrm{<mo>=</mo>1<mo>/</mo>2}$ .

Our strategy is to use the reduction to the absurd method to validate it. With this in mind, let us then assume that there exists s = a+bi∈ℂ such that a ≠ 1/2, 0 < a < 1 and such that ζ(a+bi)=0.

If the above were true, then using Proposition 1 it would also be satisfied that ζ(1-(a+bi))=0. Therefore, since the function ζ(s) is continuous ∀s∈ℂ such that Re(s)∈(0,1), then if a is, for example, less than 1-a, then this implies that $\mathrm{<mo>|</mo>}\zeta \mathrm{<mo\; stretchy="false">(</mo>}a+bi\mathrm{<mo\; stretchy="false">)</mo><mo>|</mo><mo>=</mo><mo>|</mo>}\zeta \mathrm{<mo\; stretchy="false">(</mo>1}-\mathrm{<mo\; stretchy="false">(</mo>}a+bi\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo><mo>|</mo><mo>=</mo>0}$ , and then also that $|\zeta (a+bi){|}^2=|\zeta (1-(a+bi)){|}^2=0$ . Then, $|\zeta (x+yi){|}^2$ , as a real function of real variables x and y, should have a maximum or a minimum for some x+yi∈ℂ, where 0 < a < x < 1-a< 1 (assuming, without loss of generality, that a < 1-a).

Let us now analyze if this is possible. First, notice that

$|\zeta (x+yi){|}^2=\zeta (x+yi)\overline{\zeta (x+yi)}=\zeta (x+yi)\zeta (x-yi),(10)$

Where in the last step we used Proposition 2. Next, we calculate the following first-order partial derivative with respect to x:

${\partial }_x|\zeta (x+yi){|}^2={\partial }_x\left(\zeta (x+yi)\zeta (x-yi)\right)=\left({\partial }_x\zeta (x+yi)\right)\zeta (x-yi)+\zeta (x+yi)\left({\partial }_x\zeta (x-yi)\right),$

$\mathrm{<mo>=</mo>}{\zeta }^{\prime }\mathrm{<mo\; stretchy="false">(</mo>}x+yi\mathrm{<mo\; stretchy="false">)</mo>}\zeta \mathrm{<mo\; stretchy="false">(</mo>}x-yi\mathrm{<mo\; stretchy="false">)</mo>}+\zeta \mathrm{<mo\; stretchy="false">(</mo>}x+yi\mathrm{<mo\; stretchy="false">)</mo>}{\zeta }^{\prime }\mathrm{<mo\; stretchy="false">(</mo>}x-yi\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>0.}\text{ (11)}$

This equation implies that

${\zeta }^{\prime }\mathrm{<mo\; stretchy="false">(</mo>}x+yi\mathrm{<mo\; stretchy="false">)</mo>}\zeta \mathrm{<mo\; stretchy="false">(</mo>}x-yi\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}-\zeta \mathrm{<mo\; stretchy="false">(</mo>}x+yi\mathrm{<mo\; stretchy="false">)</mo>}{\zeta }^{\prime }\mathrm{<mo\; stretchy="false">(</mo>}x-yi\mathrm{<mo\; stretchy="false">)</mo>}\Rightarrow \frac{{\zeta }^{\prime }\mathrm{<mo\; stretchy="false">(</mo>}x+yi\mathrm{<mo\; stretchy="false">)</mo>}}{\zeta \mathrm{<mo\; stretchy="false">(</mo>}x+yi\mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{<mo>=</mo>}-\frac{{\zeta }^{\prime }\mathrm{<mo\; stretchy="false">(</mo>}x-yi\mathrm{<mo\; stretchy="false">)</mo>}}{\zeta \mathrm{<mo\; stretchy="false">(</mo>}x-yi\mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{.}\text{ (12)}$

Integrating the above expression we find

$ln\left(\zeta (x+yi)\right)=ln\left({\left(\zeta (x-yi)\right)}^{-1}\right)\zeta (x+yi)=\frac{1}{\zeta (x-yi)}\zeta (x+yi)\zeta (x-yi)=1.(13)$

We can now do the same but using the first-order partial derivative with respect to y:

${\partial }_y|\zeta (x+yi){|}^2={\partial }_y\left(\zeta (x+yi)\zeta (x-yi)\right)=\left({\partial }_y\zeta (x+yi)\right)\zeta (x-yi)+\zeta (x+yi)\left({\partial }_y\zeta (x-yi)\right),$

$\mathrm{<mo>=</mo>}i\cdot {\zeta }^{\prime }\mathrm{<mo\; stretchy="false">(</mo>}x+yi\mathrm{<mo\; stretchy="false">)</mo>}\zeta \mathrm{<mo\; stretchy="false">(</mo>}x-yi\mathrm{<mo\; stretchy="false">)</mo>}-i\cdot \zeta \mathrm{<mo\; stretchy="false">(</mo>}x+yi\mathrm{<mo\; stretchy="false">)</mo>}{\zeta }^{\prime }\mathrm{<mo\; stretchy="false">(</mo>}x-yi\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>0.}\text{ (14)}$

This equation implies that

${\zeta }^{\prime }\mathrm{<mo\; stretchy="false">(</mo>}x+yi\mathrm{<mo\; stretchy="false">)</mo>}\zeta \mathrm{<mo\; stretchy="false">(</mo>}x-yi\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\zeta \mathrm{<mo\; stretchy="false">(</mo>}x+yi\mathrm{<mo\; stretchy="false">)</mo>}{\zeta }^{\prime }\mathrm{<mo\; stretchy="false">(</mo>}x-yi\mathrm{<mo\; stretchy="false">)</mo>}\Rightarrow \frac{{\zeta }^{\prime }\mathrm{<mo\; stretchy="false">(</mo>}x+yi\mathrm{<mo\; stretchy="false">)</mo>}}{\zeta \mathrm{<mo\; stretchy="false">(</mo>}x+yi\mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{<mo>=</mo>}\frac{{\zeta }^{\prime }\mathrm{<mo\; stretchy="false">(</mo>}x-yi\mathrm{<mo\; stretchy="false">)</mo>}}{\zeta \mathrm{<mo\; stretchy="false">(</mo>}x-yi\mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{.}\text{ (15)}$

Integrating the above expression we find

$\ln \left(\zeta \mathrm{<mo\; stretchy="false">(</mo>}x+yi\mathrm{<mo\; stretchy="false">)</mo>}\right)\mathrm{<mo>=</mo>}\ln \left(\zeta \mathrm{<mo\; stretchy="false">(</mo>}x-yi\mathrm{<mo\; stretchy="false">)</mo>}\right)\Rightarrow \zeta \mathrm{<mo\; stretchy="false">(</mo>}x+yi\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\zeta \mathrm{<mo\; stretchy="false">(</mo>}x-yi\mathrm{<mo\; stretchy="false">)</mo>.}\text{ (16)}$

Hence, using Eq.13 in combination with Eq.16 we have:

$\text{Re (}\zeta \text{(}x+yi{\text{))}}^{\text{2}}=1.\text{ (17)}$

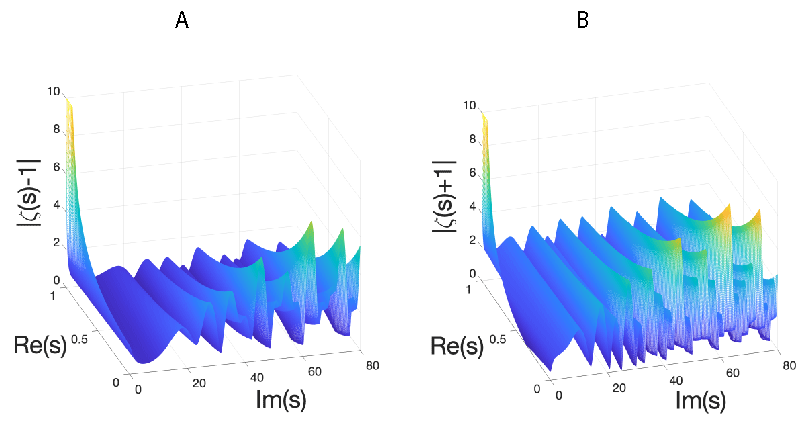
Therefore, the question is now then rephrased as if there exists an x+yi∈ℂ with 0 < a< x < 1-a< 1 and such that ζ(x+yi)=+1 or -1. Notice that if ζ(x+yi)=±1, then Re(ζ(x+yi))=±1 and Im(ζ(x+yi))=0, implying then that $\mathrm{<mo>|</mo>}\zeta \mathrm{<mo\; stretchy="false">(</mo>}x+yi\mathrm{<mo\; stretchy="false">)</mo>}\mp \mathrm{1<mo>|</mo><mo>=</mo>0}$ . In what follows we tackle whether this can be true using several methods. First, we analyzed the above condition numerically by means of extensive Matlab simulations, implementing ζ(x+yi) both in terms of its series definition and in terms of the functional equation, seeing no difference between the two implementations. We have observed that the function is symmetric with respect to y, and therefore studied it only for y≥0. In Figure 1 we show surface plots of $\mathrm{<mo>|</mo>}\zeta \mathrm{<mo\; stretchy="false">(</mo>}s\mathrm{<mo\; stretchy="false">)</mo>}\mp \mathrm{1<mo>|</mo>}$ (with s =x+yi). We see that the function is always strictly larger than zero in the considered domains. Both figures also give an intuition of what is the structure of the respective functions, with oscillations coming from the sinusoidal part in the functional definition of the zeta function.

Figure 1: Modulus of (a) ζ(s)-1 and (b) ζ(s)+1, for 0 < Re(s) < 1 and 0 < Im(s) < 80. The function is symmetric with respect to Im(s) ↔ -Im(s).

In addition, we have minimized both functions to the best of our numerical capabilities using a gradient-free Nelder-Mead algorithm with Matlab. Up to machine precision, it was impossible to find exact zeros for 0 < x < 1 (we found the minimum with magnitude around 0(10^-5)). The Matlab code is provided in Appendix A. Our analysis has also shown that it is possible to find exact zeros for x∉(0,1). For instance, using Matlab minimization with Nelder-Mead methods we could find exact zeros for $x\approx 1400$ . In addition, using WolframAlpha to solve the system of equations Re(ζ(x+yi)) = 1 and lm(ζ(x+yi))=0, we found exact zeros at values such as, (x,y)=(53.7781,9.0647),(54.8643,-4.5323),(55.2193,-9.0647),…, clearly beyond the considered domain, and with similar conclusions for the case Re(ζ(x+yi)) = -1, finding exact zeros at values such as. (x,y)=(-5.0154,5.5222),(-5.0154,-5.5222),(-3.3476,14.2831),… . Details are also provided in Appendix A. Therefore, $|\zeta (x+yi){|}^2$ does not have a maximum or a minimum for some x+yi∈ℂ with 0 < a < x < 1-a < 1, and the same happens for |ζ(x+yi)|, hence it cannot be possible that ζ(a+yi) = ζ(1-a+yi) = 0 . So, we arrive at a contradiction. This implies that if ζ(s) has any zero with 0< Re(s)< 1, then the real part cannot be different to 1/2, but instead equal to 1/2, as we wanted to prove. This observation is correct within the validity and capacity of our numerical calculations.

Next, we consider the second direction of the implication.

ii $\text{If R}e\mathrm{<mo\; stretchy="false">(</mo>}s\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>1<mo>/</mo>2} \text{ then }\exists y\in ℝ \text{such that }\zeta \mathrm{<mo\; stretchy="false">(</mo>1<mo>/</mo>2}+yi\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>0}$

To prove this statement, we should prove that ∃y∈ℝ such that ζ(1/2+yi)=0, that is, such that Re(ζ(1/2+yi))=0 and lm(ζ(1/2+yi))=0.

We use again reduction to absurdity. That is, we will assume that $\nexists y\in ℝ$ such that Re(ζ(1/2+yi)) = 0 and lm(ζ(1/2+yi))=0. And this means that by applying logic rules for the negation of quantifiers and the Morgan law to negate conjunction, we must prove that Ɐy∈ℝ it is satisfied that Re(ζ(1/2+yi)) ≠ 0 or Im(ζ(1/2+yi)) ≠0.

Hence, let us assume that Ɐy∈ℝ it is satisfied that ζ(1/2+yi) = a+bi≠0. Below we analyze if it can be satisfied that b≠0 or a≠0.

b≠0: In such case this implies that $\forall y\in ℝ$ the imaginary part has always the same sign. However, using Proposition 2, $\zeta (1/2+(-y)i)=\overline{\zeta (1/2+yi)}=\overline{a+bi}=a-bi$ . That is, Ɐy∈ℝ, we have that Im(ζ(1/2+yi)) changes its sign between -y and y. Hence, using Bolzano's theorem, it will be zero between -y and y. Therefore, we arrive at a contradiction, and this implies that ∃y∈ℝ such that the Im(ζ(1/2+yi))=b=0.

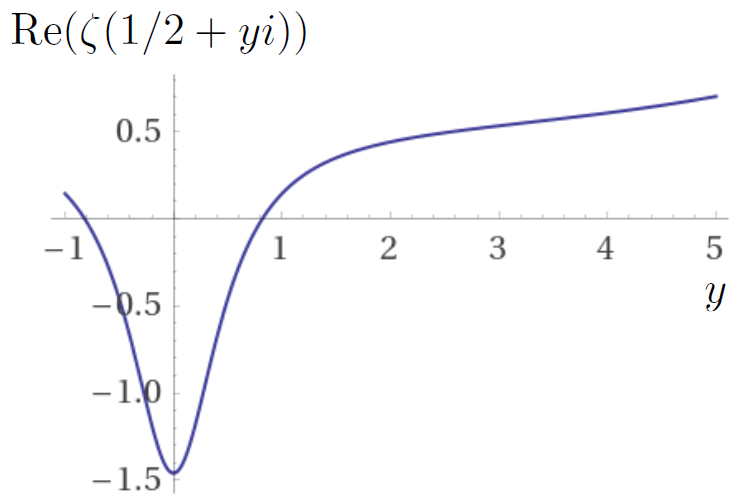
a≠0: In such case this implies that $\forall y\in ℝ$ the real part has always the same sign. However, we know that $\zeta \mathrm{<mo\; stretchy="false">(</mo>1<mo>/</mo>2<mo\; stretchy="false">)</mo><mo>=</mo>}-\mathrm{1.4603545088...}$ , and for instance, $\zeta \mathrm{<mo\; stretchy="false">(</mo>1<mo>/</mo>2}+5i\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>0.7018123711...}+\mathrm{0.2310380083...}i$ . That is, for y = 0 the real part is negative, whereas for y = 5 it is positive. Hence, using Bolzano's theorem, the real part will be zero between y = 0 and y = 5. Therefore, we arrive again at a contradiction, and this implies that ∃y∈ℝ such that Re(ζ(1/2+yi))=a=0. The plot in Figure 2 shows this case.

Figure 2: Real part of ζ(1/2+yi)for -1 < y < 5.

Therefore, in both cases, we arrive at a formal contradiction, and this implies that it cannot be possible that $\nexists y\in ℝ$ such that Re(ζ(1/2+ yi))=0 and lm(ζ(1/2+yi))=0, or what is the same, that Ɐy∈ℝ it is satisfied that Re(ζ(1/2+yi)) ≠0 or lm(ζ(1/2+yi)) ≠0.

So, this implies that ∃y∈ℝ such that ζ(1/2+yi)=0, as we wanted to prove.

Constraints on the zeros

To fine-tune the above analysis, our next question is: how are these y∈ℝ such that ζ(1/2+ yi)=0? Let us analyze this below.

Let y∈ℝ be a real number such that ζ(1/2+yi) = a+bi≠0, that is, such that the real and imaginary parts of that ζ(1/2+yi) are not simultaneously 0. Then, using the functional equation Eq.(1) we have that

$\zeta \left(\frac{1}{2}+yi\right)=a+bi=\sqrt{\frac{2}{\pi }}{(2\pi )}^{yi}sin\left(\frac{\pi }{4}+\frac{y\pi }{2}i\right)\Gamma \left(\frac{1}{2}-yi\right)\zeta \left(\frac{1}{2}-yi\right).(18)$

And using Proposition 2 we know that ζ (1/2-yi) = a-bi. So, this implies that

$a+bi=\sqrt{\frac{2}{\pi }}{(2\pi )}^{yi}sin\left(\frac{\pi }{4}+\frac{y\pi }{2}i\right)\Gamma \left(\frac{1}{2}-yi\right)(a-bi).(19)$

Then, since a-bi ≠0, we have that

$\frac{a+bi}{a-bi}=\sqrt{\frac{2}{\pi }}{(2\pi )}^{yi}sin\left(\frac{\pi }{4}+\frac{y\pi }{2}i\right)\Gamma \left(\frac{1}{2}-yi\right),$

$\frac{{(a+bi)}^2}{(a-bi)(a+bi)}=\sqrt{\frac{2}{\pi }}{(2\pi )}^{yi}sin\left(\frac{\pi }{4}+\frac{y\pi }{2}i\right)\Gamma \left(\frac{1}{2}-yi\right),$

$\frac{a^2-b^2+2abi}{a^2+b^2}=\sqrt{\frac{2}{\pi }}{(2\pi )}^{yi}sin\left(\frac{\pi }{4}+\frac{y\pi }{2}i\right)\Gamma \left(\frac{1}{2}-yi\right),$

$\frac{a^2-b^2}{a^2+b^2}+\frac{2ab}{a^2+b^2}i=\sqrt{\frac{2}{\pi }}{(2\pi )}^{yi}sin\left(\frac{\pi }{4}+\frac{y\pi }{2}i\right)\Gamma \left(\frac{1}{2}-yi\right).(20)$

Hence,

$Re\left(\sqrt{\frac{2}{\pi }}{(2\pi )}^{yi}sin\left(\frac{\pi }{4}+\frac{y\pi }{2}i\right)\Gamma \left(\frac{1}{2}-yi\right)\right)=\frac{a^2-b^2}{a^2+b^2},$

$Im\left(\sqrt{\frac{2}{\pi }}{(2\pi )}^{yi}sin\left(\frac{\pi }{4}+\frac{y\pi }{2}i\right)\Gamma \left(\frac{1}{2}-yi\right)\right)=\frac{2ab}{a^2+b^2}.(21)$

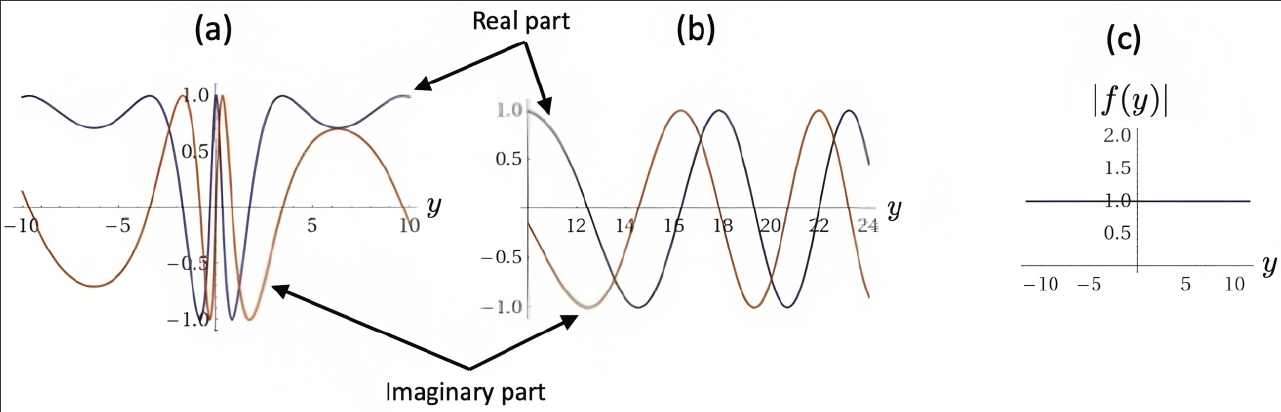
Let us now call

$f(y)=\sqrt{\frac{2}{\pi }}{(2\pi )}^{yi}sin\left(\frac{\pi }{4}+\frac{y\pi }{2}i\right)\Gamma \left(\frac{1}{2}-yi\right).(22)$

The behavior of this function is shown in Figure 3a,b. We see also in Figure 3c that the function also satisfies |f(y)|=1 for all y.

Figure 3: Function f(y) for (a) -10 < y < 10 and (b) 10 < y < 24, separated for ease of identification of different behaviour regimes. (c) Modulus |f(y)| for -10 < y < 10. The same behaviour for the modulus is observed no matter the value of y.

Then, if we call c(y)=Re(f(y)) and d(y) = lm (f(y)), since |f(y)| = 1, we have that

${(c(y))}^2+{(d(y))}^2=1.(23)$

Therefore, if c(y)=±1 then d(y) = 0, and if d(y)=±1 then c(y) = 0. If we now analyze these cases using Eq.21, we have the following:

a) Case $c\mathrm{<mo\; stretchy="false">(</mo>}y\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}-1$ and $d\mathrm{<mo\; stretchy="false">(</mo>}y\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>0}$ :

$-\mathrm{1<mo>=</mo>}\frac{a^2-b^2}{a^2+b^2}\mathrm{,}$

$\mathrm{0<mo>=</mo>}\frac{2ab}{a^2+b^2}\mathrm{.}\text{ (24)}$

That is:

$-a^2-b^2\mathrm{<mo>=</mo>}{a}^2-b^2\mathrm{,}$

$\mathrm{0<mo>=</mo>2}ab\mathrm{.}\text{ (25)}$

From the first equation we obtain a = 0 and then the second equation is always satisfied for all b, included b=0. Therefore, if c(y) = -1 and d(y) = 0, then a+bi can be equal to 0.

b) Case $c\mathrm{<mo\; stretchy="false">(</mo>}y\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>1}$ and $d\mathrm{<mo\; stretchy="false">(</mo>}y\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>0}$ :

$\mathrm{1<mo>=</mo>}\frac{a^2-b^2}{a^2+b^2}\mathrm{,}$

$\mathrm{0<mo>=</mo>}\frac{2ab}{a^2+b^2}\mathrm{.}\text{ (26)}$

That is:

$a^2+b^2\mathrm{<mo>=</mo>}{a}^2-b^2\mathrm{,}$

$\mathrm{0<mo>=</mo>2}ab\mathrm{.}\text{ (27)}$

From the first equation we obtain b = 0, and then the second equation is always satisfied for all a, included a =0. Therefore, if c(y) = 1 and d(y) = 0 then a+bi can be equal to 0.

c) Case c(y) = 0 and d(y) = 1:

$\mathrm{0<mo>=</mo>}\frac{a^2-b^2}{a^2+b^2}\mathrm{,}$

$\mathrm{1<mo>=</mo>}\frac{2ab}{a^2+b^2}\mathrm{.}\text{ (28)}$

That is:

$\mathrm{0<mo>=</mo>}{a}^2-b^2\mathrm{,}$

$a^2+b^2\mathrm{<mo>=</mo>2}ab\mathrm{.}\text{ (29)}$

From the second equation we obtain (a-b)² = 0, ie a = b, and then the first equation is always satisfied, included for a = b = 0. Therefore, if c(y) = 0 and d(y) = 1, then a+bi can be equal to 0.

d) Case $c\mathrm{<mo\; stretchy="false">(</mo>}y\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>0}$ and $d\mathrm{<mo\; stretchy="false">(</mo>}y\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}-1$ :

$\mathrm{0<mo>=</mo>}\frac{a^2-b^2}{a^2+b^2}\mathrm{,}$

$-\mathrm{1<mo>=</mo>}\frac{2ab}{a^2+b^2}\mathrm{.}\text{ (30)}$

That is:

$\mathrm{0<mo>=</mo>}{a}^2-b^2\mathrm{,}$

$-a^2-b^2\mathrm{<mo>=</mo>2}ab\mathrm{.}\text{ (31)}$

From the second equation we obtain (a+b)² = 0, ie a = -b, and then the first equation is always satisfied, included for a = b = 0. Therefore, if c(y) = 0 and d(y) = -1, then a+bi can be equal to 0.

Hence, as a consequence of the results obtained above, we can not assume that ζ(1/2+yi)=a+bi≠0 for all y∈ℝ. Therefore, ∃y∈ℝ, satisfying any of the four cases analyzed above, such that ζ(1/2+yi)=a+bi=0, as we wanted to prove.

Conclusion

In this paper, we have analyzed the Riemann hypothesis. Our objective has been, from the beginning, to validate whether this hypothesis is true or not. We did such validation using the functional equation of the zeta function, and stating that, if and only if the real part of a complex number was equal to 1/2, only then could we find a real number y such that ζ(1/2+yi) was equal to zero, so that the non-trivial zeros of the function all lie on the strip line 1/2+yi. We began our study by stating and proving two propositions. The first proposition was the key step in order to start building the whole analysis that we presented in this paper. For this analysis, we have used the functional equation of ζ(s) for s∈ℂ with 0< Re(s)< 1, and using the absurdity reduction method, we assumed that the zeros of ζ(s) can have their real part equal to a≠1/2 and 0 < a < 1, reaching a contradiction. This is obtained after an analytical study based on a complex function, and its modulus as a real function of two real variables, combined with an intensive numerical analysis up to the best of our computational resources in order to check the strict positivity of the given modulus function. Additionally, using also the absurdity reduction method, in combination with some logic rules to negate a quantifier and Morgan's law, we showed analytically that if Re(s)=1/2, then ∃y∈ℝ such that ζ(1/2+yi) = 0. Moreover, we provided analytical conditions that should be satisfied by the y values candidates, so that ζ(1/2+yi) = 0.

We need to remark again that, needless to say, the numerical analysis methods implemented with Matlab and Wolfram Alpha work under certain typical assumptions, like not exceeding a certain accepted minimum and small enough error, as well as limitations coming from potential sources of error such as rounding in floating point operations and machine precision.

This work is one more step toward assessing the validity of Riemman's conjecture. As such, we have proven here that the conjecture is true, up to the best of our numerical analysis for the strict positivity of $\mathrm{<mo>|</mo>}\zeta \mathrm{<mo\; stretchy="false">(</mo>}x+yi\mathrm{<mo\; stretchy="false">)</mo>}\mp \mathrm{1<mo>|</mo>}$ for 0 < x < 1. Our analysis shows that this function is never exactly zero in this interval, to the best of our computational power, and we see no tendency for a change. Given that the rest of the derivations here are fully analytical, this leads us to say that, to the best of our capabilities, we believe that Riemann's conjecture is true.

Appendix-A

We acknowledge Prof. Richard Taylor, from Stanford University, for an insightful comment on a previous version of this manuscript. Fruitful discussions over the years with many mathematicians and physicists' colleagues about the validity and applications of the conjecture are also acknowledged. Finally, we also acknowledge computational support from Mathworks and Wolfram.

1. Bertrand R. Ueber die Anzahl der Primzahlen unter einer gegebenen Groesse, Monatsberichte der Berliner Akademie. 1859.
2. Enrico B. The Riemann Hypothesis - official problem description (PDF), Clay Mathematics Institute. 2000; retrieved February 21, 2011. Reprinted in (Borwein, et al. 2008).
3. Guillermo LS. El problema cuya solución quizás conozcan en el cielo, Naukas. 2014. https://naukas.com/2014/05/26/el-problema-cuya-solucion-quizas-la-conozcan-en-el-cielo/https://naukas.com/2014/05/26/el-problema-cuya-solucion-quizas-la-conozcan-en-el-cielo/
4. See, for instance. https://en.wikipedia.org/wiki/Millennium_Prize_Problemshttps://en.wikipedia.org/wiki/MillenniumPrizeProblems
5. Lawrence WC, Ambrose Y. Analogues of the Robin-Lagarias Criteria for the Riemann Hypothesis, International Journal of Number Theory. 2021; 17:04; 843-870.
6. Fabrizio T, Ignazio L. Majorana quanta, string scattering, curved spacetimes and the Riemann Hypothesis, Physica Scripta. 2021; 96: 125276.
7. Giuseppe M, Andre L. Randomness of Mobius coefficients and Brownian motion: growth of the Mertens function and the Riemann Hypothesis, J. Stat. Mech. 2021; 113106.
8. Andrés C, Quesada-Herrera E. The second moment of $S_n\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}$ on the Riemann hypothesis, International Journal of Number Theory. 2022; 18:06; 1203-1226.
9. Gaugry V, Louis J, Radhakrishnan N, Michel W. On good universality and the Riemann hypothesis, Advances in Mathematics. 2021; 385:107762.
10. Panos B, Nava G, Olga P. Black holes, quantum chaos and the Riemann hypothesis, SciPost Phys. Core. 2021; 4:032.
11. André L. Riemann Hypothesis and Random Walks: the Zeta case, Symmetry. 2014; 2021:13.
12. Atul D, Shivajee G, Akshaa V. A modular relation involving non-trivial zeros of the Dedekind zeta function, and the Generalized Riemann Hypothesis, Journal of Mathematical Analysis and Applications. 2022; 515: 2; 15.
13. Norio K. An analogue of the Riemann Hypothesis via quantum walks, Quantum Studies: Mathematics and Foundations. 2022; 9:367-379.
14. Archit A, Meghali G, Bibekananda M. Proc. Amer. Math. Soc. 2022.
15. André V. Discretized Keiper/Li approach to the Riemann Hypothesis, Exp. Math. 2020; 29(4):452-469.
16. Hugues B, Yves L, Thomas R. a positivity conjecture related to the Riemann zeta function, American Mathematical Monthly. 2019; 126:891-904.
17. Goran R. Quasiperiodic sets at infinity and meromorphic extensions of their fractal zeta functions, Bull. Malays. Math. Sci. Soc. 2023; 46:107.
18. Kathrin B, Ben K. Generalized L-functions for meromorphic modular forms and their relation to the Riemann zeta function. arXiv:2112.12943.
19. Brian CJ. The Riemann Hypothesis, Notice of the AMS. 2003; 50(3):341-353.
20. Chengyan L. Riemann Hypothesis, arXiv:math/9909153.
21. Yaqing L, Deng-Shan W. Exotic wave patterns in Riemann problem of the high-order Jaulent-Miodek equation: Whitham modulation theory, Studies in Applied Mathematics. 2022; 149(3):588-630.
22. Michel B. An arithmetical function related to Báez-Duarte's criterion for the Riemann hypothesis, In: Rassias, M.T. (eds) Harmonic Analysis and Applications. Springer Optimization and Its Applications. Springer. 2021; 168.
23. André L, x Giuseppe L. Generalized Riemann Hypothesis, Time Series and Normal Distributions, J. Stat. Mech. 2019; 023203.
24. Matt V. Variants on Andrica's conjecture with and without the Riemann hypothesis, Mathematics. 2018; 6:12; 289.
25. Giuseppe M, André L. Generalized Riemann Hypothesis and Stochastic Time Series, J. Stat. Mech. 2018; 063205.
26. Ivan C. Riemann Hypothesis for DAHA superpolynomials and plane curve singularities, Communications in Number Theory and Physics. 2018; 12:3; 409-490.
27. Emanuel C, Andrés C. Bounding $S_n\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}$  on the Riemann hypothesis, Mathematical Proceedings of the Cambridge Philosophical Society. 2018; 164:259-283.
28. Sandro B, Steven GM. The  conjecture implies the Riemann hypothesis, Mathematika. 2017; 63:01; 29-33.
29. Tomoki K. The Riemann hypothesis and holomorphic index in complex dynamics, Exp. Math. 2018; 27:37-46.
30. Ade SI. Two estimates on the distribution of zeros of the first derivative of Dirichlet L-functions under the generalized Riemann hypothesis, J. Théor. Nombres Bordeaux. 2017; 29:2; 471-502.
31. Takashi N. A complete Riemann zeta distribution and the Riemann hypothesis, Bernoulli. 2015; 21:1; 604-617.
32. Eugene B. Riemann zeta function and quantum chaos, Progress of theoretical physics supplement. 2007; 166:19-44.
33. German S. A physics pathway to the Riemann hypothesis, Julio Abad "in Memoriam", edited by Manuel Asorey Carballeira, José Vicente García Esteve, Manuel F Ranada, J Sesma, 2009. ISBN 978-84-92774-04-3.
34. Remmen GN. Amplitudes and the Riemann Zeta Function. Phys Rev Lett. 2021 Dec 10;127(24):241602. doi: 10.1103/PhysRevLett.127.241602. PMID: 34951795.
35. Román O, Samuel M, Enrique L. Quantum computing for finance: overview and prospects, Reviews in Physics. 2019; 4:100028.
36. Andrew G. Harals Cramér and the distribution of prime numbers, Scandinavian Actuarial Journal. 2011; 1995:1; 12-28.
37. See, for instance, https://en.wikipedia.org/wiki/RSA_(cryptosystem)https://en.wikipedia.org/wiki/RSA(cryptosystem)
38. Peter SW. Algorithms for quantum computation: discrete logarithms and factoring, Proceedings 35th Annual Symposium on Foundations of Computer Science. IEEE Comput. Soc. Press: 1994; 124-134.
39. Paul D, Alexander A. Random matrix theory in statistics: A review, Journal of Statistical Planning and Inference. 2014; 150:1-29.
40. Xin WZ. A Survey of Large Language Models, arXiv:2303.18223.
41. Christophe J, Mercedes OL. How to extract knowledge of Qualitative Data from Big Textual Data, SCIREA Journal of Computer. 2021; 6:1; 18-53.