Mathematical analysis of the new α - difference operator with an application to prey-predator model with harvesting. Quadratic invariant

In this research paper, we introduce a novel mathematical operator known as the alpha-difference operator (α-DO) and its corresponding integral. We establish the foundational theorems related to this operator and demonstrate its applications in both linear and nonlinear dynamical equations. A key focus of our study is the application of α-DO in the context of the prey-predator model with harvesting. In the linear scenario, we derive exact solutions for the model. For the nonlinear case, we develop an iterative scheme to obtain approximate solutions. We also prove a theorem that guarantees the convergence of this scheme. We conduct a thorough investigation of the dynamical behavior of the system as the parameter varies. This is visualized through graphical representations. Our findings reveal that the system exhibits local memory, which significantly influences the evolution of the system. We observe that the α-DO is particularly effective in describing dynamical systems that undergo a change in behavior at a specific characteristic time. This is especially relevant to the system under consideration. A prime example of such a system is the Exposed-Infected-Recovery System (EIRS). Lastly, we construct the Hamiltonian function using a quadratic invariant. This provides further insights into the energy conservation and stability properties of the system. Our research opens up new insight for the application of the α-DO in various fields of science and engineering.

1. Introduction

Different prototypes of calculus, besides the classical ones, are well established. Among them, are q-calculus, fractional, proportional derivative, and variational calculus. By proportional derivatives, we mean; conformable, Beta, fractal derivatives, and M-truncated derivatives [1-3]. We mention, also, q -, fractional [4] and q - variational calculus [5]. These calculuss were employed in many trends of research in applied mathematics and in the applied sciences. They were the objective of numerous researchers as far as they are the topics of a variety of scientific journals. Many non-classical calculuss are well established in the literature. Basic and advanced analysis and also applications were approached. The q - difference (q-D) operator was introduced in [6]. In this issue, the existence of a fundamental set of n-linearly independent solutions to linear q-difference equation of order was proved in [7]. Meromorphic solutions of -difference equations (q-DE) were studied in [8,9], due to the apparent role of the existence of such solutions of finite order for the integrability of discrete difference equations. The q-DE has applications in quantum calculus (5) and in thermodynamics for entropy [10]. Also q -dynamic equation was introduced in [11-14] with applications in biology. In [9], the well-known logistic equation was studied in the quantum calculus analogue. Different forms of Fractional Derivatives (FD) have been proposed in the literature. Riemann-Liouville (RL), Caputo [15], and Caputo-Fabrizio [15-17].

A definition of the general fractional time derivative (FTD) will be defined later on, where the kernel may be chosen singular or regular. Indeed, when studying the dynamic evolution of a system with FTD, means that we are concerned with determining the effect of the distributed delay (or recent memory) on the system behavior. This may be argued to that a delay “t-t₁” that exists in the kernel. Fractional systems are used to model phenomena that exhibit anomalous or complex behaviors. This holds in systems with long memory or with hereditary effects. Fractional nonlinear PDEs were used in many areas of science, physics, biology, chemistry, and engineering sciences (Electronics and telecommunications) [18-21]. In physics, analysis, and modeling of diffusion phenomenon were currently considered. In biology and biophysics, the electrical conductance of biological systems, fractional modeling of neurons, muscle modeling, and lung modeling were studied. Fractional nonlinear dynamical systems NLDS have been studied by many researchers [22-35]. Very recently, a relevant work unified, approximately, the different forms, by reducing them to proportional derivatives [36]. The dynamics of prey-predator harvesting are currently studied in the literature. A prey–predator-type fishery model with Beddington–DeAngelis functional response and selective harvesting of predator species was considered in [37]. A prey-predator model incorporating prey-refuge and independent harvesting in either species was proposed with controlling harvesting to break the cyclic behavior of the system [38].

Bioeconomic harvesting of a prey-predator fishery in which both the species are infected by some toxicants was considered [39]. In [40], a fractional-order prey-predator model was introduced and the dynamical behavior of the system was investigated via local stability. The study of one prey and one predator harvesting model with imprecise biological parameters was presented [41]. Further relevant works were carried out [42-47].

Here, a new FDO is introduced that reveals the memory compression effect, which is relevant in dynamical systems and in computer sciences. Thus, we are led to clarify the different memory descriptions. To this issue, they can classified as (i) memory transport (time delay), (ii) memory compression, and (iii) recent or ancient- memory. Cases (ii) and (iii) are relevant in systems with time-fractional derivatives.

This paper is organized as follows.

In Sec. 2 basic definitions and memory index are presented. Sec. 3 is concerned with introducing the NDO. The ND integral operator is proposed in Sec. 4. Applications are considered in Sec. 5 and the quadratic invariant is presented in Sec. 6.. Sec. 7 is devoted to conclusions.

2. Basic definitions and memory index

2.1 Basic definitions

Definition 1: The q-difference is defined by [6]

$D_{q}f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\{\begin{array}{cc}\begin{array}{c}\frac{f\mathrm{<mo\; stretchy="false">(</mo>}qt\mathrm{<mo\; stretchy="false">)</mo>}-f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}}{t\mathrm{<mo\; stretchy="false">(</mo>}q-\mathrm{1<mo\; stretchy="false">)</mo>}}\mathrm{,}\\ \frac{f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}-f\mathrm{<mo\; stretchy="false">(</mo>}qt\mathrm{<mo\; stretchy="false">)</mo>}}{t\mathrm{<mo\; stretchy="false">(</mo>1}-q\mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{,}\\ f^{\text{'}}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>,}\end{array}& \begin{array}{c}q\mathrm{<mo>></mo>1,}\\ q\mathrm{<mo><</mo>1,}\\ q\mathrm{<mo>=</mo>1.}\end{array}\end{array}\text{ (1)}$

Definition 2 (new): The definition of the FTD in the Caputo- version, with a general (kernel regular or singular), is,

$\begin{array}{c}S\\ 0\end{array}{D}_t^{\alpha }f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}A\mathrm{<mo\; stretchy="false">(</mo>}\alpha \mathrm{<mo\; stretchy="false">)</mo>}{\displaystyle {\int }_0^t}K\mathrm{<mo\; stretchy="false">(</mo>}t-t_1\mathrm{,}\alpha \mathrm{<mo\; stretchy="false">)</mo>}{f}^{\text{'}}\mathrm{<mo\; stretchy="false">(</mo>}{t}_1\mathrm{<mo\; stretchy="false">)</mo>}d{t}_1\mathrm{,0<mo><</mo>}\alpha \mathrm{<mo><</mo>1,}\text{ (2)}$

Where $fϵC^{\mathrm{,1,}\alpha }\mathrm{<mo\; stretchy="false">(</mo>}{ℝ}^{+}\mathrm{<mo\; stretchy="false">)</mo>},C^{\mathrm{,1,}\alpha }\mathrm{<mo\; stretchy="false">(</mo>}{ℝ}^{+}\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo><mo>\{</mo>}u\mathrm{,}uϵC^1\mathrm{<mo\; stretchy="false">(</mo>}{ℝ}^{+}\mathrm{<mo\; stretchy="false">)</mo>},$ $|{\displaystyle {\int }_0^t}K\mathrm{<mo\; stretchy="false">(</mo>}t-t_1\mathrm{,}\alpha \mathrm{<mo\; stretchy="false">)</mo>}{u}^{\text{'}}\mathrm{<mo\; stretchy="false">(</mo>}{t}_1\mathrm{<mo\; stretchy="false">)</mo>}d{t}_1|\mathrm{<mo><</mo>}K\mathrm{<mo>\}</mo>.}A\mathrm{<mo\; stretchy="false">(</mo>}\alpha \mathrm{<mo\; stretchy="false">)</mo>}$ . can not be defined in general. It may be considered as a normalization factor to fit with a particular Def. of a fractional derivative.

To distinguish between these different memories that arise in dynamical systems, we define the memory index function relative to a dynamical quantity u(f(t)), t is the time variable.

A memory index function is defined as follows [11].

$M_{ind}\mathrm{<mo\; stretchy="false">(</mo>}u\mathrm{<mo\; stretchy="false">(</mo>}f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo><mo>=</mo>}Arg\mathrm{<mo\; stretchy="false">(</mo>}u\mathrm{<mo\; stretchy="false">(</mo>}f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}-t\mathrm{<mo>=</mo>}f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}-t\text{ (3)}$

We mention that when f(t)=t then M_ind(u(f(t))) = 0 and when f(t)=t+1 then M_ind(u(f(t))) = 1.

Definition 3: A system is said to be with memory if Mind(u(f(t))) < 0.

Examples

1. When  $f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}t-\tau ,M_{ind}\mathrm{<mo\; stretchy="false">(</mo>}u\mathrm{<mo\; stretchy="false">(</mo>}f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo><mo>=</mo>}-\tau \mathrm{<mo><</mo>0}$ and then the system is with local memory.
2. When  $f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{\displaystyle {\int }_0^t}{\mathrm{<mo\; stretchy="false">(</mo>}t-\tau \mathrm{<mo\; stretchy="false">)</mo>}}^{r}h\mathrm{<mo\; stretchy="false">(</mo>}\tau \mathrm{<mo\; stretchy="false">)</mo>}d\tau \mathrm{,}$ the system is with distributed memory (recent memory),
3. When $f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{\displaystyle {\int }_{-\infty }^t}{\mathrm{<mo\; stretchy="false">(</mo>}t-\tau \mathrm{<mo\; stretchy="false">)</mo>}}^{r}h\mathrm{<mo\; stretchy="false">(</mo>}\tau \mathrm{<mo\; stretchy="false">)</mo>}d\tau \mathrm{,}$ the system is with ancient memory.

Now, we consider (5) and assume that $fϵC^1\mathrm{<mo\; stretchy="false">(</mo>}{ℝ}^{+}\mathrm{<mo\; stretchy="false">)</mo>}$ , it is interesting to determine memory effects associated with the operator $D_G^{\alpha }f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}$ . Indeed by using the mean value theorem, we have

$D_t^{\alpha }u\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\frac{u\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo>}-u\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}}{t^{\alpha }-t}\mathrm{<mo>=</mo>}{u}^{\text{'}}\mathrm{<mo\; stretchy="false">(</mo>}\theta \mathrm{<mo\; stretchy="false">)</mo>,}{t}^{\alpha }\mathrm{<mo><</mo>}\theta \mathrm{<mo><</mo>}t\mathrm{.}\text{ (4)}$

From (4), we find that, $Arg\mathrm{<mo\; stretchy="false">(</mo>}{D}_t^{\alpha }u\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo><mo>=</mo>}Arg\mathrm{<mo\; stretchy="false">(</mo>}{u}^{\text{'}}\mathrm{<mo\; stretchy="false">(</mo>}\theta \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo><mo>=</mo>}\theta \mathrm{.}$ Thus $M_{ind}\mathrm{<mo>=</mo>}\theta -t.$ , Thus $t^{\alpha }-t\mathrm{<mo><</mo>}{M}_{ind}\mathrm{<mo><</mo>0,}\mathrm{0<mo><</mo>}\alpha \mathrm{<mo><</mo>1}$ , which stands for non-deterministic memory compression.

3. The new α-difference operator

In an analog to the q-difference operator (1), we present the definition of ND,

New definition 4

$D_{\alpha }^{DO}f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\{\begin{array}{c}\begin{array}{cc}\frac{f\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo>}-f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}}{t^{\alpha }-t}\mathrm{,}& \mathrm{0<mo><</mo>}\alpha \mathrm{<mo><</mo>1,0<mo><</mo>}t\mathrm{<mo><</mo>1}or\alpha \mathrm{<mo>></mo>1,}t\mathrm{<mo>></mo>1}\\ \frac{f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}-f\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo>}}{t-t^{\alpha }}\mathrm{,}& \mathrm{0<mo><</mo>}\alpha \mathrm{<mo><</mo>1,}t\mathrm{<mo>></mo>1}or\alpha \mathrm{<mo>></mo>1,0<mo><</mo>}t\mathrm{<mo><</mo>1}\\ f^{\text{'}}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>,}& \alpha \mathrm{<mo>=</mo>1,}fϵC^1\mathrm{<mo\; stretchy="false">(</mo>}{ℝ}^{+}\mathrm{<mo\; stretchy="false">)</mo>}\\ f^{\text{'}}\mathrm{<mo\; stretchy="false">(</mo>1<mo\; stretchy="false">)</mo>,}& t\mathrm{<mo>=</mo>1}\end{array}\end{array}\text{ (5)}$

We mention that (5) is an analog to (1). On the other hand, the nomenclature fractional may be referred to, as 0<α<1.

Theorem 1

(a) $D_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}+g\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo><mo>=</mo>}{D}_{\alpha }^{DO}f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}+D_{\alpha }^{DO}g\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}$ .

(b) $D_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}g\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo><mo>=</mo>}g\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo>}{D}_{\alpha }^{DO}f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}+f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}{D}_{\alpha }^{DO}g\mathrm{<mo\; stretchy="false">(</mo>}t$ )

or $D_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}g\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo><mo>=</mo>}f\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo>}{D}_{\alpha }^{DO}g\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}+g\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}{D}_{\alpha }^{DO}f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}$

(c) $D_N^{\alpha }\mathrm{<mo\; stretchy="false">(</mo>}\frac{f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}}{g\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">)</mo>}=\frac{g\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}{D}_N^{\alpha }f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}-f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}{D}_N^{\alpha }g\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}}{g\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}g\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo>}}$

(d) $D_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}f{\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}}^2\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{D}_{\alpha }^{DO}f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">(</mo>}f\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo>}+f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>.}$

(e) $D_N^{\alpha }\mathrm{<mo\; stretchy="false">(</mo>}f{\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}}^n\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{D}_{\alpha }^{DO}f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}{\displaystyle {\sum }_{j\mathrm{<mo>=</mo>0}}^{n-1}}f{\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo>}}^{j}f{\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}}^{n-j}$ .

Proof

(a) $\begin{array}{l}LHS\mathrm{<mo>=</mo>}\frac{\mathrm{<mo\; stretchy="false">(</mo>}f\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo>}+g\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}-\mathrm{<mo\; stretchy="false">(</mo>}f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}+g\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}}{t^{\alpha }-t}\\ \mathrm{<mo>=</mo>}\frac{f\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo>}-f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}}{t^{\alpha }-t}+\frac{g\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo>}-g\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}}{t^{\alpha }-t}\mathrm{<mo>=</mo>}RHS\end{array}$ .

(b) $\begin{array}{c}LHS\mathrm{<mo>=</mo>}\frac{f\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo>}g\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo>}-f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}g\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}}{t^{\alpha }-t}\mathrm{<mo>=</mo>}\frac{f\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">(</mo>}g\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo>}-g\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}+f\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">(</mo>}g\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}-f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}g\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}}{t^{\alpha }-t}\\ \mathrm{<mo>=</mo>}f\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo>}\frac{\mathrm{<mo\; stretchy="false">(</mo>}g\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo>}-g\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}}{t^{\alpha }-t}+g\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\frac{f\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo>}-f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}}{t^{\alpha }-t}\mathrm{<mo>=</mo>}RHS\mathrm{.}\end{array}$

(c) $\begin{array}{c}\begin{array}{c}LHS\mathrm{<mo>=</mo>}\frac{1}{t^{\alpha }-t}\mathrm{<mo\; stretchy="false">(</mo>}\frac{f\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo>}}{g\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo>}}-\frac{f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}}{g\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\frac{1}{g\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}g\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">(</mo>}{t}^{\alpha }-t\mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">(</mo>}f\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo>}g\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}-f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}g\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo><mo>=</mo>}\\ \frac{1}{g\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}g\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">[</mo>}\frac{\mathrm{<mo\; stretchy="false">(</mo><mo\; stretchy="false">(</mo>}f\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo>}-f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}}{\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }-t\mathrm{<mo\; stretchy="false">)</mo>}}g\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}-f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\frac{\mathrm{<mo\; stretchy="false">(</mo>}-g\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}+g\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}}{\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">(</mo>}{t}^{\alpha }-t\mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">]</mo><mo>=</mo>}RHS\end{array}\end{array}$

(d). Put g(t) = f(t) in (b)

(e) By using (d) and by induction.

The proof is completed

Now we identify the function that is invariant under the ND.

Theorem 2

The following function is invariant under the ND.

$E_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{\displaystyle \prod _{n\mathrm{<mo>=</mo>1}}^{\infty }}\frac{1}{1+|t^{{\alpha }^n}-t^{{\alpha }^{\mathrm{<mo\; stretchy="false">(</mo>}n-\mathrm{1<mo\; stretchy="false">)</mo>}}}|}\mathrm{,}t\mathrm{<mo>></mo>0,0<mo><</mo>}\alpha \mathrm{<mo><</mo>1,,}t\ne 1.\text{ (6)}$

Proof

The function which is invariant under the ND satisfies,

$D_{\alpha }^{DO}f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>.}\text{ (7)}$

First, let 0α<1Using (19) gives,

$f\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">(</mo>1}+\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }-t\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>,0<mo><</mo>}t\mathrm{<mo><</mo>1,0<mo><</mo>}\alpha \mathrm{<mo><</mo>1.}\text{ (8)}$

By iterating (8) and letting in each subsequent step, we have,

$\begin{array}{c}f\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">(</mo>1}+\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }-t\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>,}\\ f\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^2}\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}f\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">(</mo>1}+\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^2}-t^{\alpha }\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>,}\\ ⋮\\ f\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^n}\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}f\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^{\mathrm{<mo\; stretchy="false">(</mo>}n-\mathrm{1<mo\; stretchy="false">)</mo>}}}\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">(</mo>1}+\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^n}-t^{{\alpha }^{\mathrm{<mo\; stretchy="false">(</mo>}n-\mathrm{1<mo\; stretchy="false">)</mo>}}}\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>.}\end{array}\text{ (9)}$

By applying the product of both sides and as n→∞, as 0<α<1 then, αⁿ→0 and we get,

$E_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}f\mathrm{<mo\; stretchy="false">(</mo>1<mo\; stretchy="false">)</mo>}{\displaystyle \prod _{n\mathrm{<mo>=</mo>1}}^{\infty }}\frac{1}{1+\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^n}-t^{{\alpha }^{\mathrm{<mo\; stretchy="false">(</mo>}n-\mathrm{1<mo\; stretchy="false">)</mo>}}}\mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{,}\mathrm{0<mo><</mo>}t\mathrm{<mo><</mo>1,0<mo><</mo>}\alpha \mathrm{<mo><</mo>1.}\text{ (10)}$

Second, let t>1,0<α<1 and by the same way, we find,

$E_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}f\mathrm{<mo\; stretchy="false">(</mo>1<mo\; stretchy="false">)</mo>}{\displaystyle \prod _{n\mathrm{<mo>=</mo>1}}^{\infty }}\frac{1}{1+\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^{n-1}}-t^{{\alpha }^n}\mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{,}t\mathrm{<mo>></mo>1,0<mo><</mo>}\alpha \mathrm{<mo><</mo>1.}\text{ (11)}$

Here, we take f(1)=1. From (10) and (11), we get (6).

This completes the proof .

Now, consider the equation,

$D_{\alpha }^{DO}f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\lambda f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>,}\lambda \mathrm{<mo>=</mo>}-ib\mathrm{.}\text{ (12)}$

The solution of (12) is,

$\begin{array}{c}{E}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{,}-ib\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{\displaystyle \prod _{n\mathrm{<mo>=</mo>1}}^{\infty }}\frac{1}{1+{\mathrm{<mo\; stretchy="false">(</mo>}-ib|\mathrm{<mo\; stretchy="false">)</mo>}}^{{}^n}{t}^{{\alpha }^n}-t^{{\alpha }^{\mathrm{<mo\; stretchy="false">(</mo>}n-\mathrm{1<mo\; stretchy="false">)</mo>}}}|}\mathrm{<mo>=</mo>}\\ \\ {\displaystyle \prod _{m\mathrm{<mo>=</mo>1}}^{\infty }}\frac{1}{\mathrm{<mo\; stretchy="false">(</mo>1}+b^{2m}|t^{{\alpha }^{2m}}-t^{{\alpha }^{\mathrm{<mo\; stretchy="false">(</mo>2}m-\mathrm{1<mo\; stretchy="false">)</mo>}}}{|}^2\mathrm{<mo\; stretchy="false">)</mo>}}+i{\displaystyle \prod _{m\mathrm{<mo>=</mo>1}}^{\infty }}\frac{b^m|t^{{\alpha }^{2m+1}}-t^{{\alpha }^{2m\mathrm{<mo\; stretchy="false">)</mo>}}}|}{\mathrm{<mo\; stretchy="false">(</mo>1}+b^{2m}|t^{{\alpha }^{2m+1}}-t^{{\alpha }^{2m\mathrm{<mo\; stretchy="false">)</mo>}}}{|}^2\mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{.}\end{array}\text{ (13)}$

Eq. (13) suggests to write,

$\begin{array}{l}co{s}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{,}b\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{\displaystyle \prod _{m\mathrm{<mo>=</mo>1}}^{\infty }}\frac{1}{\mathrm{<mo\; stretchy="false">(</mo>1}+b^{2m}|t^{{\alpha }^{2m}}-t^{{\alpha }^{\mathrm{<mo\; stretchy="false">(</mo>2}m-\mathrm{1<mo\; stretchy="false">)</mo>}}}{|}^2\mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{,}\hfill \\ \hfill \\ si{n}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{,}b\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{\displaystyle \prod _{m\mathrm{<mo>=</mo>0}}^{\infty }}\frac{b^m|t^{{\alpha }^{2m+1}}-t^{{\alpha }^{2m\mathrm{<mo\; stretchy="false">)</mo>}}}|}{\mathrm{<mo\; stretchy="false">(</mo>1}+b^{2m}|t^{{\alpha }^{2m+1}}-t^{{\alpha }^{2m\mathrm{<mo\; stretchy="false">)</mo>}}}{|}^2\mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{,}t\mathrm{<mo>></mo>0,}\mathrm{0<mo><</mo>}\alpha \mathrm{<mo><</mo>1.}\hfill \end{array}\text{ (14)}$

In the same way, we define,

$\begin{array}{l}cos{h}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{,}b\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\frac{1}{2}\mathrm{<mo\; stretchy="false">(</mo>}{E}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{,}b\mathrm{<mo\; stretchy="false">)</mo>}+E_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{,}-b\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo><mo>=</mo>}{\displaystyle \prod _{m\mathrm{<mo>=</mo>1}}^{\infty }}\frac{1}{\mathrm{<mo\; stretchy="false">(</mo>1}-b^{2m}|t^{{\alpha }^{2m}}-t^{{\alpha }^{\mathrm{<mo\; stretchy="false">(</mo>2}m-\mathrm{1<mo\; stretchy="false">)</mo>}}}{|}^2\mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{,}\hfill \\ \hfill \\ sin{h}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{,}b\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\frac{1}{2}\mathrm{<mo\; stretchy="false">(</mo>}{E}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{,}b\mathrm{<mo\; stretchy="false">)</mo>}-E_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{,}-b\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo><mo>=</mo>}{\displaystyle \prod _{m\mathrm{<mo>=</mo>0}}^{\infty }}\frac{b^m|t^{{\alpha }^{2m+1}}-t^{{\alpha }^{2m\mathrm{<mo\; stretchy="false">)</mo>}}}|}{\mathrm{<mo\; stretchy="false">(</mo>1}-b^{2m}|t^{{\alpha }^{2m+1}}-t^{{\alpha }^{2m\mathrm{<mo\; stretchy="false">)</mo>}}}{|}^2\mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{,}t\mathrm{<mo>></mo>0,}\mathrm{0<mo><</mo>}\alpha \mathrm{<mo><</mo>1.}\hfill \end{array}\text{ (15)}$

We remark that $E_{\alpha }^{Do}\mathrm{<mo\; stretchy="false">(</mo>0,}b\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>1,}co{s}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>0,}b\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>1,}cos{h}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>0,}b\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>1,}si{n}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>0,}b\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>0}$ and $sin{h}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>0,}b\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>0}$ .

3.1 Higher order fractional difference

We have,

$\begin{array}{l}{D}_{2\alpha }^{DO}f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{D}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}{D}_{\alpha }^{DO}f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo><mo>=</mo>}{D}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}\frac{f\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo>}-f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}}{t^{\alpha }-t}\mathrm{<mo\; stretchy="false">)</mo>}\hfill \\ \hfill \\ \mathrm{<mo>=</mo>}\frac{f\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^2}\mathrm{<mo\; stretchy="false">)</mo>}-f\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo>}}{t^{{\alpha }^2}-t^{\alpha }}-\frac{f\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo>}-f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}}{t^{\alpha }-t}\mathrm{<mo>=</mo>}{D}_N^{\alpha }\mathrm{<mo\; stretchy="false">(</mo>}f\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}-D_N^{\alpha }\mathrm{<mo\; stretchy="false">(</mo>}f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>,}\hfill \\ D_{3\alpha }^{DO}f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{D}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}{D}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}{D}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo><mo>=</mo>}{D}_{2\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}f\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}-D{2}_{\alpha }^{DO}f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>,}\hfill \\ ⋮\hfill \\ \underset{D_{n\alpha }^{DO}f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\stackrel{}{\overbrace{D_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}{D}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>....}{D}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}}}\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{D}_{\mathrm{<mo\; stretchy="false">(</mo>}n-\mathrm{1<mo\; stretchy="false">)</mo>}\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}f\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}-D_{\mathrm{<mo\; stretchy="false">(</mo>}n-\mathrm{1<mo\; stretchy="false">)</mo>}\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>.}}{n}\hfill \end{array}\text{ (16)}$

When $fϵC^1\mathrm{<mo\; stretchy="false">(</mo>}{ℝ}^{+}\mathrm{<mo\; stretchy="false">)</mo>}$ , the ND mean value theorem states,

$\begin{array}{c}\mathrm{<mo\; stretchy="false">(</mo>}i\mathrm{<mo\; stretchy="false">)</mo>}\frac{f\mathrm{<mo\; stretchy="false">(</mo>}{a}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo>}-f\mathrm{<mo\; stretchy="false">(</mo>}a\mathrm{<mo\; stretchy="false">)</mo>}}{a^{\alpha }-a}\mathrm{<mo>=</mo>}{f}^{\text{'}}\mathrm{<mo\; stretchy="false">(</mo>}\xi \mathrm{<mo\; stretchy="false">)</mo>,}{a}^{\alpha }\mathrm{<mo><</mo>}\xi \mathrm{<mo><</mo>}a\mathrm{,}\mathrm{0<mo><</mo>}t\mathrm{<mo><</mo>1,}\mathrm{0<mo><</mo>}\alpha \mathrm{<mo><</mo>1}ort\mathrm{<mo>></mo>1,}\alpha \mathrm{<mo>></mo>1,}\\ \\ \mathrm{<mo\; stretchy="false">(</mo>}ii\mathrm{<mo\; stretchy="false">)</mo>}\frac{f\mathrm{<mo\; stretchy="false">(</mo>}a\mathrm{<mo\; stretchy="false">)</mo>}-f\mathrm{<mo\; stretchy="false">(</mo>}{a}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo>}}{a-a^{\alpha }}\mathrm{<mo>=</mo>}{f}^{\text{'}}\mathrm{<mo\; stretchy="false">(</mo>}\xi \mathrm{<mo\; stretchy="false">)</mo>,}a\mathrm{<mo><</mo>}\xi \mathrm{<mo><</mo>}{a}^{\alpha }\mathrm{,}t\mathrm{<mo>></mo>1,}\mathrm{0<mo><</mo>}\alpha \mathrm{<mo><</mo>1}or\mathrm{0<mo><</mo>}t\mathrm{<mo><</mo>1,}\alpha \mathrm{<mo>></mo>1.}\end{array}\text{ (17)}$

Example. Consider the function f(t)=tⁿ.

$\begin{array}{l}{D}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}{t}^n\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\frac{t^{n\alpha }-t^n}{t^{\alpha }-t}\mathrm{<mo>=</mo>}{\displaystyle \sum _{j\mathrm{<mo>=</mo>0}}^{n-1}}{t}^{j\alpha }{t}^{n-1-j}\mathrm{<mo>=</mo>}{t}^{n-1}{e}_n^{\alpha }\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>,}\hfill \\ \hfill \\ e_n^{\alpha }\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{\displaystyle \sum _{j\mathrm{<mo>=</mo>0}}^{n-1}}{t}^{j\mathrm{<mo\; stretchy="false">(</mo>}\alpha -\mathrm{1<mo\; stretchy="false">)</mo>}}\mathrm{,}t\mathrm{<mo>></mo>0,}\alpha \mathrm{<mo>></mo>0}or\alpha \mathrm{<mo>></mo>1,}t\ge 0.\hfill \end{array}\text{ (18)}$

In (17), we put f(t)=tⁿ, in this case, we find that,

$\xi \mathrm{<mo>=</mo><mo\; stretchy="false">(</mo>}\frac{a^{n-1}{e}_n^{\alpha }\mathrm{<mo\; stretchy="false">(</mo>}a\mathrm{<mo\; stretchy="false">)</mo>}}{n}{\mathrm{<mo\; stretchy="false">)</mo>}}^{\frac{1}{n-1}}\mathrm{,}n\mathrm{<mo>></mo>1.}\text{ (19)}$

4.α-DO integral operator and applications

We proceed to define the ND-integral by considering the ND equation.

We consider a basic equation,

$D_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}g\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo><mo>=</mo>}K\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>.,}t\mathrm{<mo>></mo>0,}\mathrm{0<mo><</mo>}\alpha \mathrm{<mo><</mo>1.}\text{ (20)}$

For the solution of (20), we have the following theorem.

Theorem 3

The solution of (20) is,

$g\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}g\mathrm{<mo\; stretchy="false">(</mo>1<mo\; stretchy="false">)</mo>}-{\displaystyle \sum _{k\mathrm{<mo>=</mo>1}}^{\infty }}|t^{{\alpha }^k}-t^{{\alpha }^{k-1}}|K\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^{k-1}}\mathrm{<mo\; stretchy="false">)</mo>,}t\mathrm{<mo>></mo>0,}\mathrm{0<mo><</mo>}\alpha \mathrm{<mo><</mo>1.}\text{ (21)}$

Proof

First, let 0α<1 and rewrite (20) in the form,

$g\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo>}-g\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}K\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">(</mo>}{t}^{\alpha }-t\mathrm{<mo\; stretchy="false">)</mo>.}\text{ (22)}$

It is worth mentioning that (22) is a functional equation. By using the same steps, as was done in (6), we have,

$\begin{array}{c}g\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo>}-g\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}K\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">(</mo>}{t}^{\alpha }-t\mathrm{<mo\; stretchy="false">)</mo>,}\\ g\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^2}\mathrm{<mo\; stretchy="false">)</mo>}-g\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}K\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">(</mo>}{t}^{{\alpha }^2}-t^{\alpha }\mathrm{<mo\; stretchy="false">)</mo>,}\\ ⋮\\ g\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^k}\mathrm{<mo\; stretchy="false">)</mo>}-g\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^{k-1}}\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}K\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^{k-1}}\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">(</mo>}{t}^{{\alpha }^k}-t^{{\alpha }^{k-1}}\mathrm{<mo\; stretchy="false">)</mo>.}\end{array}\text{ (23)}$

Summing both sides of (23) and letting k →∞, we get,

$g\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}g\mathrm{<mo\; stretchy="false">(</mo>1<mo\; stretchy="false">)</mo>}-{\displaystyle \sum _{k\mathrm{<mo>=</mo>1}}^{\infty }}\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^k}-t^{{\alpha }^{k-1}}\mathrm{<mo\; stretchy="false">)</mo>}K\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^{k-1}}\mathrm{<mo\; stretchy="false">)</mo>,0<mo><</mo>}t\mathrm{<mo><</mo>1,}\mathrm{0<mo><</mo>}\alpha \mathrm{<mo><</mo>1.}\text{ (24)}$

The second case is dealt with in the same way and we get,

$g\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}g\mathrm{<mo\; stretchy="false">(</mo>1<mo\; stretchy="false">)</mo>}-{\displaystyle \sum _{k\mathrm{<mo>=</mo>1}}^{\infty }}\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^{k--1}}-t^{{\alpha }^k}\mathrm{<mo\; stretchy="false">)</mo>}K\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^{k-1}}\mathrm{<mo\; stretchy="false">)</mo>,}t\mathrm{<mo>></mo>1,}\mathrm{0<mo><</mo>}\alpha \mathrm{<mo><</mo>1,}\text{ (25)}$

By using (24) and (25), we get (21) and the proof is completed .

4.1 α-DO integral

Indeed, the solution of (20) can be written symbolically,

$g\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{I}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}K\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\{\begin{array}{cc}g\mathrm{<mo\; stretchy="false">(</mo>1<mo\; stretchy="false">)</mo>}+{\displaystyle {\int }_t^1}K\mathrm{<mo\; stretchy="false">(</mo>}{t}_1\mathrm{<mo\; stretchy="false">)</mo>}{d}_{\alpha }{t}_1\mathrm{,}& \mathrm{0<mo><</mo>}t\le \mathrm{1,}\\ g\mathrm{<mo\; stretchy="false">(</mo>1<mo\; stretchy="false">)</mo>}+{\displaystyle {\int }_1^t}K\mathrm{<mo\; stretchy="false">(</mo>}{t}_1\mathrm{<mo\; stretchy="false">)</mo>}{d}_{\alpha }{t}_1\mathrm{,}& t\ge 1.\end{array}\text{ (26)}$

By using (21) and (25), the α-DO integral definite integrals are defined by,

Definition 5

$\begin{array}{c}{\displaystyle {\int }_t^1}K\mathrm{<mo\; stretchy="false">(</mo>}{t}_1\mathrm{<mo\; stretchy="false">)</mo>}{d}_{\alpha }{t}_1\mathrm{<mo>=</mo>}{\displaystyle \sum _{k\mathrm{<mo>=</mo>1}}^{\infty }}\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^k}-t^{{\alpha }^{k-1}}\mathrm{<mo\; stretchy="false">)</mo>}K\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^{k-1}}\mathrm{<mo\; stretchy="false">)</mo>,}\mathrm{0<mo><</mo>}t\mathrm{<mo><</mo>1,}\mathrm{0<mo><</mo>}\alpha \mathrm{<mo><</mo>1,}\\ \\ {\displaystyle {\int }_1^t}K\mathrm{<mo\; stretchy="false">(</mo>}{t}_1\mathrm{<mo\; stretchy="false">)</mo>}{d}_{\alpha }{t}_1\mathrm{<mo>=</mo>}{\displaystyle \sum _{k\mathrm{<mo>=</mo>1}}^{\infty }}\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^{k-1}}-t^{{\alpha }^k}\mathrm{<mo\; stretchy="false">)</mo>}K\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^{k-1}}\mathrm{<mo\; stretchy="false">)</mo>,}t\mathrm{<mo>></mo>1,}\mathrm{0<mo><</mo>}\alpha \mathrm{<mo><</mo>1.}\end{array}\text{ (27)}$

We can rewrite (27) by,

${\displaystyle {\int }_0^t}K\mathrm{<mo\; stretchy="false">(</mo>}{t}_1\mathrm{<mo\; stretchy="false">)</mo>}{d}_{\alpha }{t}_1\mathrm{<mo>=</mo>}{\displaystyle \sum _{k\mathrm{<mo>=</mo>1}}^{\infty }}|t^{{\alpha }^k}-t^{{\alpha }^{k-1}}|K\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^{k-1}}\mathrm{<mo\; stretchy="false">)</mo>,}t\mathrm{<mo>></mo>0,}\mathrm{0<mo><</mo>}\alpha \mathrm{<mo><</mo>1.}\text{ (28)}$

Further, we have,

$\begin{array}{c}{\displaystyle {\int }_a^b}f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}d{t}_{\alpha }\mathrm{<mo>=</mo>}{\displaystyle {\int }_1^b}f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}d{t}_{\alpha }-{\displaystyle {\int }_1^a}f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}d{t}_{\alpha }\mathrm{,}b\mathrm{<mo>></mo>}a\mathrm{<mo>></mo>1,}\\ \\ {\displaystyle {\int }_a^b}f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}d{t}_{\alpha }\mathrm{<mo>=</mo>}{\displaystyle {\int }_b^1}f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}d{t}_{\alpha }-{\displaystyle {\int }_a^1}f\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}d{t}_{\alpha }\mathrm{,}a\mathrm{<mo><</mo>}b\mathrm{<mo><</mo>1.}\end{array}\text{ (29)}$

Further identities for definite integrals hold.

$\begin{array}{c}{\displaystyle {\int }_t^1}f\mathrm{<mo\; stretchy="false">(</mo>}s\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">(</mo>}{D}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo><mo\; stretchy="false">(</mo>}g\mathrm{<mo\; stretchy="false">(</mo>}s\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}{d}_{\alpha }s\mathrm{<mo>=</mo>}{\displaystyle \sum _{k\mathrm{<mo>=</mo>1}}^{\infty }}\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^k}-t^{{\alpha }^{k-1}}\mathrm{<mo\; stretchy="false">)</mo>}f\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^{k-1}}\mathrm{<mo\; stretchy="false">)</mo>}{D}_N^{\alpha }\mathrm{<mo\; stretchy="false">(</mo>}g\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^{k-1}}\mathrm{<mo\; stretchy="false">)</mo>}\\ \\ \mathrm{<mo>=</mo>}{\displaystyle \sum _{k\mathrm{<mo>=</mo>1}}^{\infty }}f\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^{k-1}}\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">(</mo>}g\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^k}\mathrm{<mo\; stretchy="false">)</mo>}-g\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^{k-1}}\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>,}\\ \\ {\displaystyle {\int }_1^t}f\mathrm{<mo\; stretchy="false">(</mo>}s\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">(</mo>}{D}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo><mo\; stretchy="false">(</mo>}g\mathrm{<mo\; stretchy="false">(</mo>}s\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}{d}_{\alpha }s\mathrm{<mo>=</mo>}{\displaystyle \sum _{k\mathrm{<mo>=</mo>1}}^{\infty }}\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^{k-1}}-t^{{\alpha }^k}\mathrm{<mo\; stretchy="false">)</mo>}f\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^k}\mathrm{<mo\; stretchy="false">)</mo>}{D}_G^{\alpha }\mathrm{<mo\; stretchy="false">(</mo>}g\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^k}\mathrm{<mo\; stretchy="false">)</mo>}\\ \\ \mathrm{<mo>=</mo>}{\displaystyle \sum _{k\mathrm{<mo>=</mo>1}}^{\infty }}f\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^k}\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">(</mo>}g\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^{k-1}}\mathrm{<mo\; stretchy="false">)</mo>}-g\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^k}\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>.}\end{array}\text{ (30)}$

$\begin{array}{c}{\displaystyle {\int }_t^1}\mathrm{<mo\; stretchy="false">(</mo>}{D}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}f\mathrm{<mo\; stretchy="false">(</mo>}s\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}{d}_{\alpha }s\mathrm{<mo>=</mo>}{\displaystyle {\int }_t^1}\frac{f\mathrm{<mo\; stretchy="false">(</mo>}{s}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo>}-f\mathrm{<mo\; stretchy="false">(</mo>}s\mathrm{<mo\; stretchy="false">)</mo>}}{s^{\alpha }-s}{d}_{\alpha }s\mathrm{<mo>=</mo>}{\displaystyle \sum _{k\mathrm{<mo>=</mo>1}}^{\infty }}\mathrm{<mo\; stretchy="false">(</mo>}f\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^k}\mathrm{<mo\; stretchy="false">)</mo>}-f\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^{k-1}}\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>,}\\ \\ {\displaystyle {\int }_1^t}\mathrm{<mo\; stretchy="false">(</mo>}{D}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}f\mathrm{<mo\; stretchy="false">(</mo>}s\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}{d}_{\alpha }s\mathrm{<mo>=</mo>}{\displaystyle {\int }_1^t}\frac{f\mathrm{<mo\; stretchy="false">(</mo>}{s}^{\alpha }\mathrm{<mo\; stretchy="false">)</mo>}-f\mathrm{<mo\; stretchy="false">(</mo>}s\mathrm{<mo\; stretchy="false">)</mo>}}{s^{\alpha }-s}{d}_{\alpha }s\mathrm{<mo>=</mo>}{\displaystyle \sum _{k\mathrm{<mo>=</mo>1}}^{\infty }}\mathrm{<mo\; stretchy="false">(</mo>}f\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^{k-1}}\mathrm{<mo\; stretchy="false">)</mo>}-f\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^k}\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>.}\end{array}\text{ (31)}$

5. Applications

As the function which is invariant under the FDO is obtained in (6), it establishes a calculus. So, it can be used to handle linear fractional difference equations.

5.1 The -DO linear dynamical system.

We consider the system,

$\begin{array}{c}{D}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}x\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}ax\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}+by\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>,}{D}_N^{\alpha }y\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}cx\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}+dy\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>.}\end{array}\text{ (32)}$

To solve (32), let $x\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{c}_1{E}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{,}\lambda \mathrm{<mo\; stretchy="false">)</mo>}$ and $y\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{c}_2{E}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{,}\lambda \mathrm{<mo\; stretchy="false">)</mo>}$ . Direct calculation gives,

and the eigenvalues are,

${\lambda }_{\mathrm{1,2}}\mathrm{<mo>=</mo>}\frac{1}{2}\mathrm{<mo\; stretchy="false">(</mo>}a+d\pm \sqrt{{\mathrm{<mo\; stretchy="false">(</mo>}a-d\mathrm{<mo\; stretchy="false">)</mo>}}^2+4bc}\mathrm{<mo\; stretchy="false">)</mo>.}\text{ (33)}$

We focus our attention on the case when (a-d)²+4bc<0. Thus we have,

$\begin{array}{c}x\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{E}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{,}\frac{\mathrm{<mo\; stretchy="false">(</mo>}a+d\mathrm{<mo\; stretchy="false">)</mo>}}{2}\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">(</mo>}x\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}co{s}_{\alpha }^{Do}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{,}r\mathrm{<mo\; stretchy="false">)</mo>}+y\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}si{n}_N^{DO}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{,}r\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>,}\\ \\ y\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{E}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{,}\frac{\mathrm{<mo\; stretchy="false">(</mo>}a+d\mathrm{<mo\; stretchy="false">)</mo>}}{2}\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">(</mo>}y\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}co{s}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{,}r\mathrm{<mo\; stretchy="false">)</mo>}+x\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}si{n}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{,}r\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>,}\\ r\mathrm{<mo>=</mo>}\frac{1}{2}\sqrt{-{\mathrm{<mo\; stretchy="false">(</mo>}a-d\mathrm{<mo\; stretchy="false">)</mo>}}^2-bc}\mathrm{,}bc\mathrm{<mo><</mo>}-{\mathrm{<mo\; stretchy="false">(</mo>}a-d\mathrm{<mo\; stretchy="false">)</mo>}}^2\mathrm{.}\end{array}\text{ (34)}$

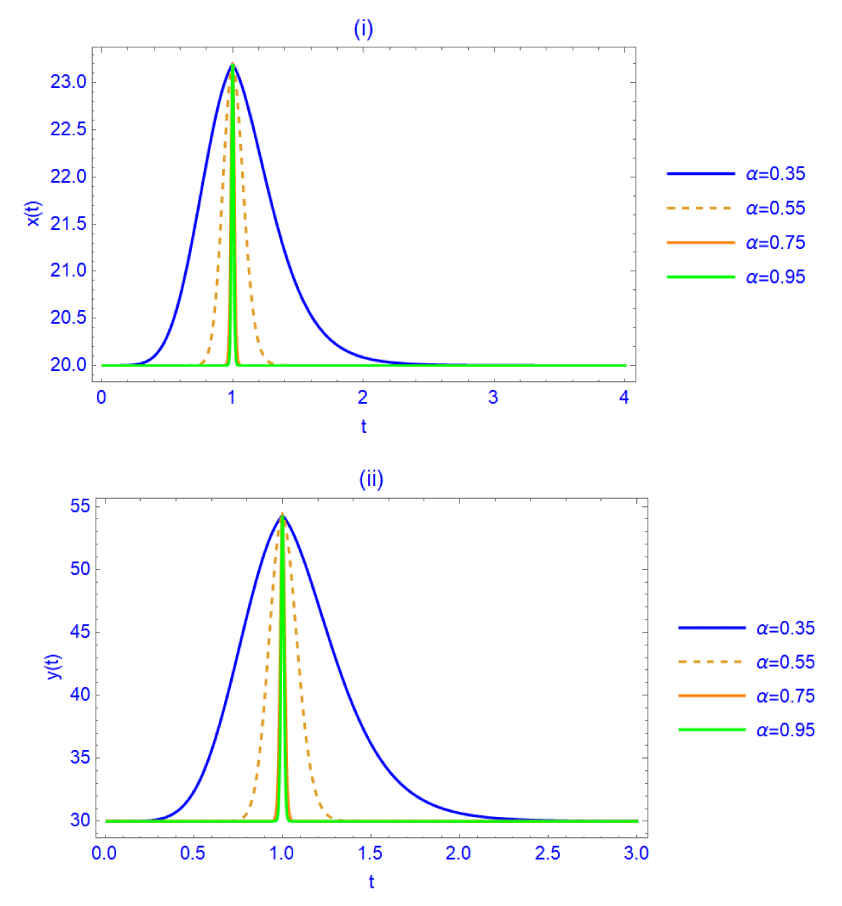
The solutions in (34) are displayed against t for different values of α in Figures 1 (i) and (ii).

We remark that the maximum value holds at t = 1 and the solutions increase when 01, while they decrease when t > 1.

It is worth mentioning that when studying real phenomena, and by considering t normalized by characteristic time τ_c, the physical quantity attains its maximum or minimum at τ_c. This illustrates the importance of the use of this new difference operator in dynamical systems.

5.2 The - DO logistic equation

Consider the ND logistic equation which is characterized by the normalized growth and death rates, and by the carrier capacity,

$D_{\alpha }^{DO}u\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\lambda u\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\mathrm{<mo\; stretchy="false">(</mo>1}-u\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>,}u\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo><mo>=</mo>}{u}_0\text{ (35)}$

Indeed, (35) is a nonlinear equation.

The solution of (35) is,

$u\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{I}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}K\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\{\begin{array}{cc}u\mathrm{<mo\; stretchy="false">(</mo>1<mo\; stretchy="false">)</mo>}+{\displaystyle {\int }_t^1}K\mathrm{<mo\; stretchy="false">(</mo>}{t}_1\mathrm{<mo\; stretchy="false">)</mo>}{d}_{\alpha }{t}_1\mathrm{,}& \mathrm{0<mo><</mo>}t\le \mathrm{1,}\\ u\mathrm{<mo\; stretchy="false">(</mo>1<mo\; stretchy="false">)</mo>}+{\displaystyle {\int }_1^t}K\mathrm{<mo\; stretchy="false">(</mo>}{t}_1\mathrm{<mo\; stretchy="false">)</mo>}{d}_{\alpha }{t}_1\mathrm{,}& t\ge \mathrm{1,}\\ K\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\lambda u\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\mathrm{<mo\; stretchy="false">(</mo>1}-u\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>.}& \end{array}\text{ (36)}$

By using (28), leads to,

$\begin{array}{c}u\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{\displaystyle \sum _{k\mathrm{<mo>=</mo>1}}^{\infty }}|t^{{\alpha }^k}-t^{{\alpha }^{k-1}}|\lambda u\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^{k-1}}\mathrm{<mo\; stretchy="false">)</mo>}\mathrm{<mo\; stretchy="false">(</mo>1}-u\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^{k-1}}\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>,}t\mathrm{<mo>></mo>0,}\mathrm{0<mo><</mo>}\alpha \mathrm{<mo><</mo>1.}\end{array}\text{ (37)}$

Here, to find the solution to (35) a discretization and an iterative scheme in (34) are used. So, we have,

$u^{\mathrm{<mo\; stretchy="false">(</mo>}n\mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{\displaystyle \sum _{k\mathrm{<mo>=</mo>1}}^{\infty }}|t^{{\alpha }^k}-t^{{\alpha }^{k-1}}|\lambda u^{\mathrm{<mo\; stretchy="false">(</mo>}n-\mathrm{1<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^{k-1}}\mathrm{<mo\; stretchy="false">)</mo>}\mathrm{<mo\; stretchy="false">(</mo>1}-u^{\mathrm{<mo\; stretchy="false">(</mo>}n-\mathrm{1<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^{k-1}}\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>,}t\mathrm{<mo>></mo>0,}\mathrm{0<mo><</mo>}\alpha \mathrm{<mo><</mo>1,}\text{ (38)}$

Where,

$u^{\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}u\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}{\displaystyle \prod _{n\mathrm{<mo>=</mo>1}}^{\infty }}\frac{1}{1+{\lambda }^n|t^{{\alpha }^{n-1}}-t^{{\alpha }^n}|}\mathrm{,}\text{ (39)}$

Thus, the first approximate solution of (35) is,

$u^{\mathrm{<mo\; stretchy="false">(</mo>1<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{\displaystyle \sum _{k\mathrm{<mo>=</mo>1}}^{\infty }}|t^{{\alpha }^k}-t^{{\alpha }^{k-1}}|\lambda u^{\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^{k-1}}\mathrm{<mo\; stretchy="false">)</mo>}\mathrm{<mo\; stretchy="false">(</mo>1}-u^{\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">(</mo>}{t}^{{\alpha }^{k-1}}\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>,}t\mathrm{<mo>></mo>0,}\mathrm{0<mo><</mo>}\alpha \mathrm{<mo><</mo>1,}\text{ (40)}$

Finally, we have,

$\begin{array}{c}{u}^{\mathrm{<mo\; stretchy="false">(</mo>1<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{\displaystyle \sum _{k\mathrm{<mo>=</mo>1}}^{\infty }}|t^{{\alpha }^k}-t^{{\alpha }^{k-1}}|\lambda u\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}{\displaystyle \prod _{n\mathrm{<mo>=</mo>1}}^{\infty }}\frac{1}{1+{\lambda }^n|t^{{\alpha }^{k+n-1}}-t^{{\alpha }^{k+n-2}}|}\\ \mathrm{<mo\; stretchy="false">(</mo>1}-u\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}{\displaystyle \prod _{n\mathrm{<mo>=</mo>1}}^{\infty }}\frac{1}{1+{\lambda }^n|t^{{\alpha }^{k+n-1}}-t^{{\alpha }^{k+n-2}}|}\mathrm{<mo\; stretchy="false">)</mo>,}t\mathrm{<mo>></mo>0,}\mathrm{0<mo><</mo>}\alpha \mathrm{<mo><</mo>1.}\end{array}\text{ (41)}$

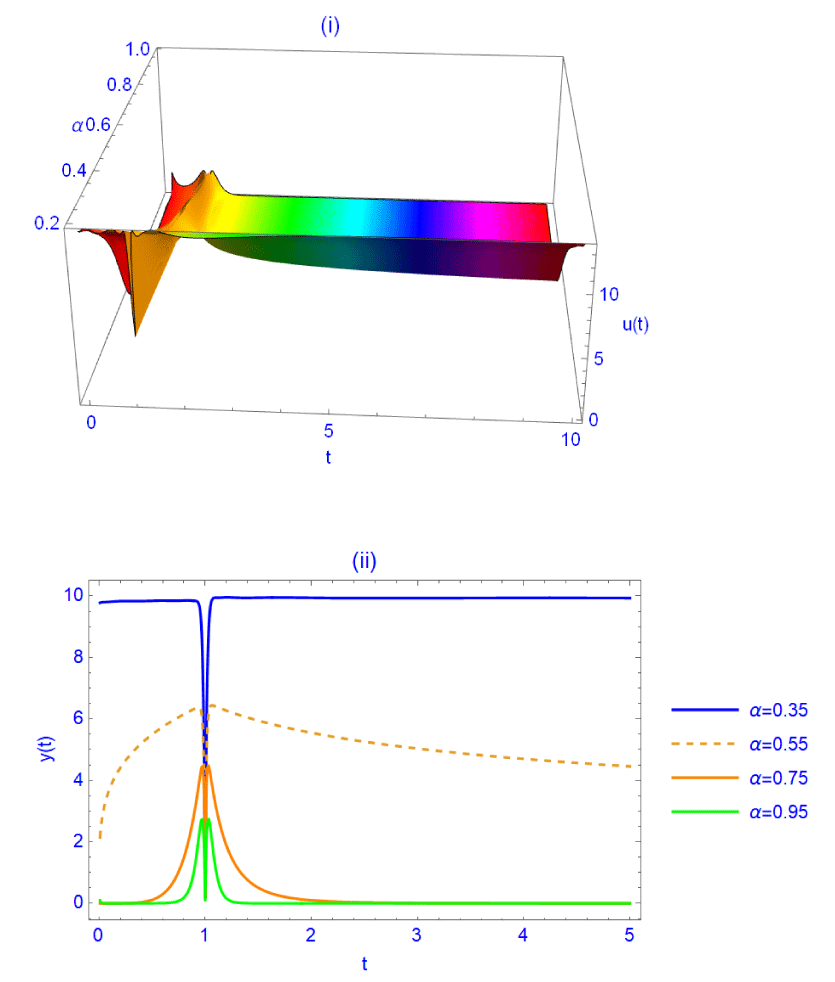
The results for the first approximation in (41) are displayed in Figures 2 (i) and (ii).

Figures 2 (i) and (ii) show that the solution of the logistic equation attains a steady state value asymptotically. We remark that the behavior of the solution, at t=1, changes significantly, which reveals that, there is a critical where the behavior changes remarkably.

5.3 The prey-predator mode

1. To construct a model for a hypothetical dynamical system, the ordinary derivative is used.
2. For modeling a dynamical system of living creatures, careful attention has to be taken into account, as a living being has a history. For example in a prey-predator model with harvesting, For a prey in order to be predated or harvested, it must exist not at time t but at time (t-t₀) and this corresponds to time delay (or local memory). Further memory aspect that describes recent history (memory) or ancient history (memory) are represented by the integrals.a

${\displaystyle {\int }_0^t}K\mathrm{<mo\; stretchy="false">(</mo>}t-t_1\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">(</mo>.<mo\; stretchy="false">)</mo>}d{t}_1\mathrm{,}{\displaystyle {\int }_{-\infty }^t}K\mathrm{<mo\; stretchy="false">(</mo>}t-t_1\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">(</mo>.<mo\; stretchy="false">)</mo>}{d}_1\mathrm{.}$

Thus, in this case, to model a dynamical system, the ordinary derivative is not realistic and it is replaced by introducing a fractional derivative. The most realistic ones are the Riemann-Liouville and Caputo derivatives [15]. It is worth mentioning that, here, the fractional difference in (19) is with fractional local memory (t^α-t), 0<α<1 (see the examples in section 2.2).

We consider the prey-predator model with proportional harvesting in the prey and predator.

Let u(t) and v(t) be, respectively, the prey and predator densities at time t.

• Assume that the prey population grows logistically with an intrinsic growth rate λ in the absence of a predator.
• Let γ be the food-independent death rate.

$\begin{array}{c}{D}_{\alpha }^{DO}u\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\lambda u\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\mathrm{<mo\; stretchy="false">(</mo>1}-u\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}-\beta u\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}v\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}-{\mu }_{1}u\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>,}\\ D_{\alpha }^{DO}v\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}-\gamma +\beta u\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}v\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}-{\mu }_{2}v\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>,}u\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo><mo>=</mo>}{u}_0\mathrm{,}v\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo><mo>=</mo>}{v}_0\mathrm{,}\end{array}\text{ (42)}$

Where µ_I,i =1,2 are the proportional harvesting coefficients, while β is the perdition rate of the prey.

Eq.(42) is written in the matrix form,

$\left(\begin{array}{c}{D}_{\alpha }^{DO}u\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\\ D_{\alpha }^{DO}v\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\end{array}\right)\mathrm{<mo>=</mo>}M\left(\begin{array}{c}u\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\\ v\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\end{array}\right)+\left(\begin{array}{c}-\beta u\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}v\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\\ -\gamma +\beta u\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}v\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\end{array}\right)\mathrm{,}M\mathrm{<mo>=</mo>}\left(\begin{array}{cc}\lambda -{\mu }_1& 0\\ 0& -{\mu }_2\end{array}\right)\mathrm{.}\text{ (43)}$

We use the transformation,

$\left(\begin{array}{c}u\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\\ v\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\end{array}\right)\mathrm{<mo>=</mo>}\left(\begin{array}{cc}{E}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{,}\lambda -{\mu }_1\mathrm{<mo\; stretchy="false">)</mo>}& 0\\ 0& E_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{,}-{\mu }_2\mathrm{<mo\; stretchy="false">)</mo>}\end{array}\right)\left(\begin{array}{c}U\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\\ V\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\end{array}\right)\mathrm{,}\text{ (44)}$

into (43) and we get,

$\begin{array}{c}\left(\begin{array}{c}{D}_{\alpha }^{DO}U\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\\ D_{\alpha }^{DO}V\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\end{array}\right)\mathrm{<mo>=</mo>}{\tilde{M}}^{-1}\left(\begin{array}{c}-\beta E_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{,}\lambda -{\mu }_1\mathrm{<mo\; stretchy="false">)</mo>}{E}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{,}-{\mu }_2\mathrm{<mo\; stretchy="false">)</mo>}U\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}V\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\\ -\gamma +\beta E_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{,}\lambda -{\mu }_1\mathrm{<mo\; stretchy="false">)</mo>}{E}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{,}-{\mu }_2\mathrm{<mo\; stretchy="false">)</mo>}U\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}V\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\end{array}\right)\mathrm{<mo>=</mo>}\\ \\ \left(\begin{array}{c}-\frac{\beta E_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{,}\lambda -{\mu }_1\mathrm{<mo\; stretchy="false">)</mo>}{E}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{,}-{\mu }_2\mathrm{<mo\; stretchy="false">)</mo>}}{E_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{,}\lambda -{\mu }_1\mathrm{<mo\; stretchy="false">)</mo>}{E}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{,}-{\mu }_2\mathrm{<mo\; stretchy="false">)</mo>}}U\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}V\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\\ -\gamma +\frac{\beta E_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{,}\lambda -{\mu }_1\mathrm{<mo\; stretchy="false">)</mo>}{E}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{,}-{\mu }_2\mathrm{<mo\; stretchy="false">)</mo>}}{E_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{,}-{\mu }_2\mathrm{<mo\; stretchy="false">)</mo>}{E}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{,}\lambda -{\mu }_1\mathrm{<mo\; stretchy="false">)</mo>}}U\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}V\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\end{array}\right)\mathrm{,}\\ \\ \tilde{M}\mathrm{<mo>=</mo>}\left(\begin{array}{cc}{E}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{,}\lambda -{\mu }_1\mathrm{<mo\; stretchy="false">)</mo>}& 0\\ 0& E_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}{t}^{\alpha }\mathrm{,}-{\mu }_2\mathrm{<mo\; stretchy="false">)</mo>}\end{array}\right)\mathrm{.}\\ \\ \end{array}\text{ (45)}$

By using (26), (45) is integrated to,

$\left(\begin{array}{c}U\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\\ V\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\end{array}\right)\mathrm{<mo>=</mo>}\left(\begin{array}{c}{u}_0\\ v_0\end{array}\right)+{\displaystyle {\int }_0^t}\left(\begin{array}{c}-\frac{\beta E_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}{t}_1\mathrm{,}\lambda -{\mu }_1\mathrm{<mo\; stretchy="false">)</mo>}{E}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}{t}_1\mathrm{,}-{\mu }_2\mathrm{<mo\; stretchy="false">)</mo>}}{E_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}{t}_1^{\alpha }\mathrm{,}\lambda -{\mu }_1\mathrm{<mo\; stretchy="false">)</mo>}{E}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}{t}_1^{\alpha }\mathrm{,}-{\mu }_2\mathrm{<mo\; stretchy="false">)</mo>}}U\mathrm{<mo\; stretchy="false">(</mo>}{t}_1\mathrm{<mo\; stretchy="false">)</mo>}V\mathrm{<mo\; stretchy="false">(</mo>}{t}_1\mathrm{<mo\; stretchy="false">)</mo>}\\ -\gamma +\frac{\beta E_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}{t}_1\mathrm{,}\lambda -{\mu }_1\mathrm{<mo\; stretchy="false">)</mo>}{E}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{,}-{\mu }_2\mathrm{<mo\; stretchy="false">)</mo>}}{E_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}{t}_1^{\alpha }\mathrm{,}\lambda -{\mu }_1\mathrm{<mo\; stretchy="false">)</mo>}{E}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}{t}_1^{\alpha }\mathrm{,}-{\mu }_2\mathrm{<mo\; stretchy="false">)</mo>}}U\mathrm{<mo\; stretchy="false">(</mo>}{t}_1\mathrm{<mo\; stretchy="false">)</mo>}V\mathrm{<mo\; stretchy="false">(</mo>}{t}_1\mathrm{<mo\; stretchy="false">)</mo>}\end{array}\right)d_{\alpha }{t}_1\mathrm{.}\text{ (46)}$

A discretization for (46) is,

$\left(\begin{array}{c}{U}^{\mathrm{<mo\; stretchy="false">(</mo>}n\mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\\ V^{\mathrm{<mo\; stretchy="false">(</mo>}n\mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\end{array}\right)\mathrm{<mo>=</mo>}\left(\begin{array}{c}{u}_0\\ v_0\end{array}\right)+{\displaystyle {\int }_0^t}\left(\begin{array}{c}-\frac{\beta E_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}{t}_1\mathrm{,}\lambda -{\mu }_1\mathrm{<mo\; stretchy="false">)</mo>}{E}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}{t}_1\mathrm{,}-{\mu }_2\mathrm{<mo\; stretchy="false">)</mo>}}{E_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}{t}_1^{\alpha }\mathrm{,}\lambda -{\mu }_1\mathrm{<mo\; stretchy="false">)</mo>}{E}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}{t}_1^{\alpha }\mathrm{,}-{\mu }_2\mathrm{<mo\; stretchy="false">)</mo>}}{U}^{\mathrm{<mo\; stretchy="false">(</mo>}n-\mathrm{1<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">(</mo>}{t}_1\mathrm{<mo\; stretchy="false">)</mo>}{V}^{\mathrm{<mo\; stretchy="false">(</mo>}n-\mathrm{1<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">(</mo>}{t}_1\mathrm{<mo\; stretchy="false">)</mo>}\\ -\gamma +\frac{E_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}{t}_1\mathrm{,}\lambda -{\mu }_1\mathrm{<mo\; stretchy="false">)</mo>}{E}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}{t}_1\mathrm{,}-{\mu }_2\mathrm{<mo\; stretchy="false">)</mo>}}{E_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}{t}_1^{\alpha }\mathrm{,}\lambda -{\mu }_1\mathrm{<mo\; stretchy="false">)</mo>}{E}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}{t}_1^{\alpha }\mathrm{,}-{\mu }_2\mathrm{<mo\; stretchy="false">)</mo>}}{U}^{\mathrm{<mo\; stretchy="false">(</mo>}n-\mathrm{1<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">(</mo>}{t}_1\mathrm{<mo\; stretchy="false">)</mo>}{V}^{\mathrm{<mo\; stretchy="false">(</mo>}n-\mathrm{1<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">(</mo>}{t}_1\mathrm{<mo\; stretchy="false">)</mo>}\end{array}\right)d_{\alpha }{t}_1\mathrm{,}\text{ (47)}$

Where $U^{\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{u}_0$ and $V^{\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{v}_0$ .

The first approximation in (47) is,

$\left(\begin{array}{c}{U}^{\mathrm{<mo\; stretchy="false">(</mo>1<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\\ V^{\mathrm{<mo\; stretchy="false">(</mo>1<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\end{array}\right)\mathrm{<mo>=</mo>}\left(\begin{array}{c}{u}_0\\ v_0\end{array}\right)+{\displaystyle {\int }_0^t}\left(\begin{array}{c}-\frac{\beta E_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}{t}_1\mathrm{,}\lambda -{\mu }_1\mathrm{<mo\; stretchy="false">)</mo>}{E}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}{t}_1\mathrm{,}-{\mu }_2\mathrm{<mo\; stretchy="false">)</mo>}}{E_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}{t}_1^{\alpha }\mathrm{,}\lambda -{\mu }_1\mathrm{<mo\; stretchy="false">)</mo>}{E}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}{t}_1^{\alpha }\mathrm{,}-{\mu }_2\mathrm{<mo\; stretchy="false">)</mo>}}{u}_0{v}_0\\ -\gamma +\frac{\beta E_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}{t}_1\mathrm{,}\lambda -{\mu }_1\mathrm{<mo\; stretchy="false">)</mo>}{E}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}{t}_1\mathrm{,}-{\mu }_2\mathrm{<mo\; stretchy="false">)</mo>}}{E_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}{t}_1^{\alpha }\mathrm{,}\lambda -{\mu }_1\mathrm{<mo\; stretchy="false">)</mo>}{E}_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}{t}_1^{\alpha }\mathrm{,}-{\mu }_2\mathrm{<mo\; stretchy="false">)</mo>}}{u}_0{v}_0\end{array}\right)d_{\alpha }{t}_1\mathrm{,}\text{ (48)}$

together with using (44).

To prove the convergence of the iterated scheme (47), first, we use (6) and find that $E_{\alpha }^{DO}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\le {\displaystyle {\prod }_{n\mathrm{<mo>=</mo>1}}^{\infty }}\frac{1}{1+t^{{\alpha }^n}}\le e^t\mathrm{,}t\mathrm{<mo>></mo>0}$ . Thus, it is sufficient to prove the convergence in the classical case.

$black\dot{U}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\left(\begin{array}{c}\dot{u}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\\ \dot{v}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\end{array}\right)\mathrm{<mo>=</mo>}M\left(\begin{array}{c}u\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\\ v\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\end{array}\right)+\left(\begin{array}{c}-\beta u\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}v\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\\ -\gamma +\beta u\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}v\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\end{array}\right)\mathrm{,}M\mathrm{<mo>=</mo>}\left(\begin{array}{cc}\lambda -{\mu }_1& 0\\ 0& -{\mu }_2\end{array}\right)\mathrm{.}\text{ (49)}$

The iteration scheme of (49) is,

$\begin{array}{c}{U}^{\mathrm{<mo\; stretchy="false">(</mo>}n\mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\left(\begin{array}{c}{u}_0\\ v_0\end{array}\right)+{\displaystyle {\int }_0^t}{e}^{-M{t}_1}\left(\begin{array}{c}-\beta u^{\mathrm{<mo\; stretchy="false">(</mo>}n-\mathrm{1<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">(</mo>}{t}_1\mathrm{<mo\; stretchy="false">)</mo>}{v}^{\mathrm{<mo\; stretchy="false">(</mo>}n-\mathrm{1<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">(</mo>}{t}_1\mathrm{<mo\; stretchy="false">)</mo>}\\ -\gamma +\beta u^{\mathrm{<mo\; stretchy="false">(</mo>}n-\mathrm{1<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">(</mo>}{t}_1\mathrm{<mo\; stretchy="false">)</mo>}{v}^{\mathrm{<mo\; stretchy="false">(</mo>}n-\mathrm{1<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">(</mo>}{t}_1\mathrm{<mo\; stretchy="false">)</mo>}\end{array}\right)d{t}_1\mathrm{,}n\ge 1.\end{array}\text{ (50)}$

Now, we prove the convergence theorem. To this issue, we present the following.

We write $U^{\mathrm{<mo\; stretchy="false">(</mo>}n\mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{<mo>=</mo><mo>\{</mo>}{U}_i^{\mathrm{<mo\; stretchy="false">(</mo>}n\mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{,}i\mathrm{<mo>=</mo>1,2,3<mo>\}</mo>,}$ where $\parallel U^{\mathrm{<mo\; stretchy="false">(</mo>}n\mathrm{<mo\; stretchy="false">)</mo>}}\parallel \mathrm{<mo>=</mo>}Ma{x}_{i\mathrm{<mo>=</mo>1,2,3}}\parallel U_i^{\mathrm{<mo\; stretchy="false">(</mo>}n\mathrm{<mo\; stretchy="false">)</mo>}}\parallel \mathrm{,}\parallel U_i^{\mathrm{<mo\; stretchy="false">(</mo>}n\mathrm{<mo\; stretchy="false">)</mo>}}\parallel \mathrm{<mo>=</mo>}Su{p}_{tϵ{ℝ}^{+}}\left|U^{\mathrm{<mo\; stretchy="false">(</mo>}n\mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\right|$

We assume that the space of solutions $S\mathrm{<mo>=</mo><mo>\{</mo>}{U}_i^{\mathrm{<mo\; stretchy="false">(</mo>}n\mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{<mo>:</mo>}{U}_i^{\mathrm{<mo\; stretchy="false">(</mo>}n\mathrm{<mo\; stretchy="false">)</mo>}}ϵC^1\mathrm{<mo\; stretchy="false">(</mo>}{ℝ}^{+}\mathrm{<mo\; stretchy="false">)</mo>,}\mathrm{,}i\mathrm{<mo>=</mo>1,2,3,}nϵ\mathbb{N}\mathrm{<mo>\}</mo>}$ is endowed by the norm

$\parallel S\parallel \mathrm{<mo>=</mo>}Ma{x}_i\parallel U_i^{\mathrm{<mo\; stretchy="false">(</mo>}n\mathrm{<mo\; stretchy="false">)</mo>}}\parallel \mathrm{,}\parallel U_i^{\mathrm{<mo\; stretchy="false">(</mo>}n\mathrm{<mo\; stretchy="false">)</mo>}}\parallel \mathrm{<mo>=</mo>}Su{p}_{tϵ{ℝ}^{+}}\left|U_i^{\mathrm{<mo\; stretchy="false">(</mo>}n\mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\right|$ ) (cf. (47)).

Define the mapping $\tilde{M}\mathrm{<mo>:</mo>}S\to S;M\mathrm{<mo\; stretchy="false">(</mo>}{u}_i^{\mathrm{<mo\; stretchy="false">(</mo>}n-\mathrm{1<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo><mo>=</mo>}{u}_i^{\mathrm{<mo\; stretchy="false">(</mo>}n\mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>.}$ We proceed with the proof of the convergence theorem by the following.

The logarithmic norm of a matrix M, which is defined by,

$\mu \mathrm{<mo\; stretchy="false">(</mo>}M\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}Limi{t}_{\delta \to 0}\frac{\parallel I+\delta M\parallel -1}{\delta }\mathrm{,}\text{ (51)}$

Where, $\parallel M\parallel$ is the matrix norm. Here, we consider $\parallel M{\parallel }_{\infty }\mathrm{<mo>=</mo>}Ma{x}_{1\le i\le n}\mathrm{<mo\; stretchy="false">(</mo>}{\displaystyle {\sum }_{{}_{j\mathrm{<mo>=</mo>1}}}^{j\mathrm{<mo>=</mo>}n}}\left|m_{{}_{ij}}\right|\mathrm{<mo\; stretchy="false">)</mo>}$

Lemma: The norm of exponential matrix $M_{m\times m}\mathrm{<mo>=</mo><mo\; stretchy="false">(</mo>}{m}_{ij}),i,j\text{=1,}\mathrm{...}\text{,}m$ satisfies [45,46],

$\parallel exp\mathrm{<mo\; stretchy="false">(</mo>}-tM\mathrm{<mo\; stretchy="false">)</mo>}{\parallel }_{\infty }\mathrm{<mo><</mo>}exp\mathrm{<mo\; stretchy="false">(</mo>}-t{\mu }_{\infty }\mathrm{<mo\; stretchy="false">(</mo>}M\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>,}\text{ (52)}$

Where ${\mu }_{\infty }\mathrm{<mo\; stretchy="false">(</mo>}M\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}Ma{x}_i\mathrm{<mo\; stretchy="false">(</mo>}\left|m_{ii}\right|+{\displaystyle {\sum }_{j\mathrm{<mo>=</mo>1,}j\ne i}^{j\mathrm{<mo>=</mo>}m}}\left|m_{ij}\right|\mathrm{<mo\; stretchy="false">)</mo>}$ .

Theorem: The sequence of solutions u⁽ⁿ⁾ converges absolutely to the exact solution black U as n →∞. as

Proof. By using (49), (50), and the lemma, we have,

$\begin{array}{c}\parallel U^{\mathrm{<mo\; stretchy="false">(</mo>1<mo\; stretchy="false">)</mo>}}-U^{\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}}\parallel \mathrm{<mo><</mo>}\parallel {\displaystyle {\int }_0^t}{e}^{-M{t}_1}\left(\begin{array}{c}-\beta u^{\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}}{v}^{\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}}\\ \gamma +\beta u^{\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}}{v}^{\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}}\end{array}\right)d{t}_1\parallel \mathrm{<mo><</mo>}\\ \\ {\displaystyle {\int }_0^t}\parallel e^{-M{t}_1}\parallel \parallel \left(\begin{array}{c}-\alpha u^{\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}}{v}^{\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}}\\ \gamma +\alpha u^{\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}}{v}^{\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}}\end{array}\right)\parallel d{t}_1\mathrm{<mo><</mo>}{\displaystyle {\int }_0^t}\parallel e^{-\mu \mathrm{<mo\; stretchy="false">(</mo>}M\mathrm{<mo\; stretchy="false">)</mo>}}\parallel \parallel \left(\begin{array}{c}-\beta u^{\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}}{v}^{\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}}\\ \gamma +\beta u^{\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}}{v}^{\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}}\end{array}\right)\parallel d{t}_1\mathrm{<mo>=</mo>}\\ \\ {\displaystyle {\int }_0^t}{e}^{-\mathrm{<mo\; stretchy="false">(</mo>}|\lambda -{\mu }_1|+\left|{\mu }_2\right|\mathrm{<mo\; stretchy="false">)</mo>}{t}_1}\parallel \left(\begin{array}{c}-\beta u^{\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}}{v}^{\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}}\\ \gamma +\beta u^{\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}}{v}^{\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}}\end{array}\right)\parallel d{t}_1\mathrm{.}\end{array}\text{ (53)}$

From (53), there exist ε0 < 1 and T₀ such that,

$\parallel U^{\mathrm{<mo\; stretchy="false">(</mo>1<mo\; stretchy="false">)</mo>}}-U^{\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}}\parallel \mathrm{<mo><</mo>}{\epsilon }_0\mathrm{<mo><</mo>1,}t\mathrm{<mo>></mo>}{T}_0\mathrm{.}\text{ (54)}$

Define a mapping $\tilde{M}$ with $\tilde{M}\mathrm{<mo\; stretchy="false">(</mo>}{U}^{\mathrm{<mo\; stretchy="false">(</mo>}i\mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{U}^{\mathrm{<mo\; stretchy="false">(</mo>}i+\mathrm{1<mo\; stretchy="false">)</mo>}}$

In the same way for $\parallel U^{\mathrm{<mo\; stretchy="false">(</mo>2<mo\; stretchy="false">)</mo>}}-U^{\mathrm{<mo\; stretchy="false">(</mo>1<mo\; stretchy="false">)</mo>}}\parallel \mathrm{<mo>=</mo>}\parallel \tilde{M}\mathrm{<mo\; stretchy="false">(</mo>}{U}^{\mathrm{<mo\; stretchy="false">(</mo>1}}\mathrm{<mo\; stretchy="false">)</mo>}-\tilde{M}\mathrm{<mo\; stretchy="false">(</mo>}{U}^{\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">)</mo>}\parallel$ it holds that there exists ε1 < 1 and T₁ such that,

$\parallel \tilde{M}\mathrm{<mo\; stretchy="false">(</mo>}{U}^{\mathrm{<mo\; stretchy="false">(</mo>1<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">)</mo>}-\tilde{M}\mathrm{<mo\; stretchy="false">(</mo>}{U}^{\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">)</mo>}\parallel \mathrm{<mo><</mo>}{\epsilon }_1\mathrm{<mo><</mo>1,}t\mathrm{<mo>></mo>}{T}_1\mathrm{,}\text{ (55)}$

and by induction, it holds that,

$\parallel \tilde{M}\mathrm{<mo\; stretchy="false">(</mo>}{U}^{\mathrm{<mo\; stretchy="false">(</mo>}n\mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">)</mo>}-\tilde{M}\mathrm{<mo\; stretchy="false">(</mo>}{U}^{n-\mathrm{1<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">)</mo>}\parallel \mathrm{<mo><</mo>}{\epsilon }_n\mathrm{<mo><</mo>1,}t\mathrm{<mo>></mo>}{T}_n\mathrm{.}\text{ (56)}$

From (54)-(56), there exist $ϵ\mathrm{<mo>=</mo>}Mi{n}_j{\epsilon }_j$ and $T\mathrm{<mo>=</mo>}Ma{x}_j{T}_j$ such that,

$\parallel \tilde{M}\mathrm{<mo\; stretchy="false">(</mo>}{U}^{\mathrm{<mo\; stretchy="false">(</mo>}n\mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">)</mo>}-\tilde{M}\mathrm{<mo\; stretchy="false">(</mo>}{U}^{n-\mathrm{1<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">)</mo>}\parallel \mathrm{<mo><</mo>}\epsilon \mathrm{<mo><</mo>1,}t\mathrm{<mo>></mo>}T\mathrm{.}\text{ (57)}$

Thus, $\tilde{M}$ is a contraction mapping. This completes the proof .

Corollary. The sequence of solutions u⁽ⁿ⁾ converges absolutely on [0,T] to the exact solution u of (3).

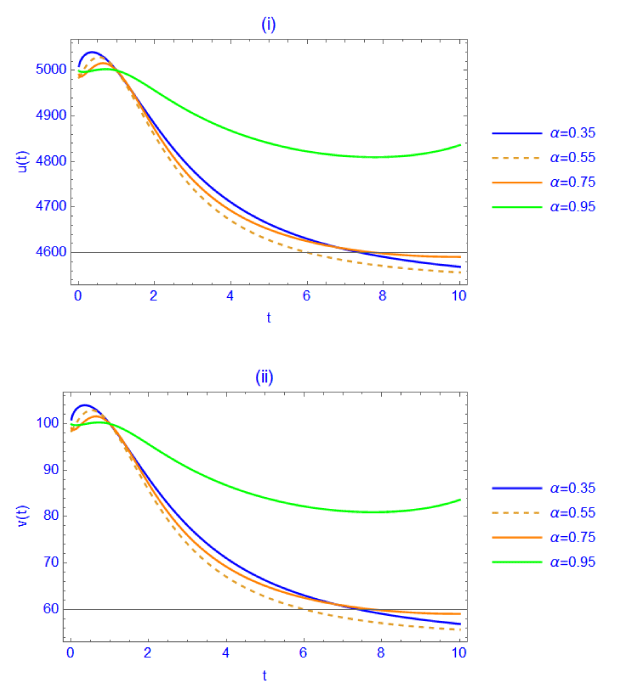
By using (6), the results in (48) are displayed in Figures. 3(i) and (ii).

When β=0.05, u0 = 5000, v0 = 100, µ1 = 0.01, µ2 = 0.005,γ = 0.001, λ = 0.5.

After Figures 3 (i) and (ii), we find that the solutions u(t) and v(t) decay with α when 0α when t>1 A global behavior of the density of the two species is to decay with time.

6. Quadratic invariant

Here, we are concerned with constructing a quadratic invariant (QI) for (56), which is a quadratic polynomial in u′(t) and v′(t) and it leads to the Hamiltonian function. Indeed, a QI for the dynamical system,

$\begin{array}{c}{u}^{\prime }\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\text{=}\lambda \mathrm{<mo\; stretchy="false">(</mo>1}-u\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}u\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}-{\mu }_{1}u\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}-\beta u\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}v\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>,}\\ v^{\prime }\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\text{=}-\gamma +\beta u\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}v\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}-{\mu }_{2}v\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>,}\end{array}\text{ (58)}$

undergoes the form,

$A_5{u^{\prime }}^2+A_4{u}^{\prime }{v}^{\prime }+A_3{v^{\prime }}^2+A_2\mathrm{<mo\; stretchy="false">(</mo>}u\mathrm{,}v\mathrm{<mo\; stretchy="false">)</mo>}{u}^{\prime }+A_1\mathrm{<mo\; stretchy="false">(</mo>}u\mathrm{,}v\mathrm{<mo\; stretchy="false">)</mo>}{v}^{\prime }+A_0\mathrm{<mo\; stretchy="false">(</mo>}u\mathrm{,}v\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>0.}\text{ (59)}$

Eq. (75) is rewritten,

$\begin{array}{c}{u^{\prime }}^{\prime }\text{=}\lambda \mathrm{<mo\; stretchy="false">(</mo>1}-2u\mathrm{<mo\; stretchy="false">)</mo>}{u}^{\prime }-{\mu }_1{u}^{\prime }-\beta v{u}^{\prime }-\beta u{v}^{\prime }\mathrm{,}\\ {v^{\prime }}^{\prime }\mathrm{<mo>=</mo>}\beta v{u}^{\prime }+\beta u{v}^{\prime }-{\mu }_2{v}^{\prime }\mathrm{.}\end{array}\text{ (60)}$

By differentiating (76), using (77), and by setting the coefficients of u′^j v′ⁱ,i,j = 0,1,2 equal to zero, we get,

$\begin{array}{c}{A}_{2u}\mathrm{<mo\; stretchy="false">(</mo>}u\mathrm{,}v\mathrm{<mo\; stretchy="false">)</mo>}\text{=}-2A_5\lambda +2A_5{\mu }_1+4A_5\lambda u+2A_5\beta v-A_4\beta v\mathrm{,}\\ A_{1u}\mathrm{<mo\; stretchy="false">(</mo>}u\mathrm{,}v\mathrm{<mo\; stretchy="false">)</mo>}\text{=}{A}_4\mathrm{<mo\; stretchy="false">(</mo>}-\lambda \mathrm{<mo\; stretchy="false">)</mo>}+A_4{\mu }_1+A_4{\mu }_2-A_4\beta u+2A_5\beta u+2A_4\lambda u\\ -A_{2v}\mathrm{<mo\; stretchy="false">(</mo>}u\mathrm{,}v\mathrm{<mo\; stretchy="false">)</mo>}-2A_3\beta v+A_4\beta v\mathrm{,}\\ A_{0u}\mathrm{<mo\; stretchy="false">(</mo>}u\mathrm{,}v\mathrm{<mo\; stretchy="false">)</mo>}\text{=}-\beta v{A}_1\mathrm{<mo\; stretchy="false">(</mo>}u\mathrm{,}v\mathrm{<mo\; stretchy="false">)</mo>}-\lambda A_2\mathrm{<mo\; stretchy="false">(</mo>}u\mathrm{,}v\mathrm{<mo\; stretchy="false">)</mo>}\beta v+A_2\mathrm{<mo\; stretchy="false">(</mo>}u\mathrm{,}v\mathrm{<mo\; stretchy="false">)</mo>}+\\ 2\lambda u{A}_2\mathrm{<mo\; stretchy="false">(</mo>}u\mathrm{,}v\mathrm{<mo\; stretchy="false">)</mo>}+{\mu }_1{A}_2\mathrm{<mo\; stretchy="false">(</mo>}u\mathrm{,}v\mathrm{<mo\; stretchy="false">)</mo>,}\\ A_{1v}\mathrm{<mo\; stretchy="false">(</mo>}u\mathrm{,}v\mathrm{<mo\; stretchy="false">)</mo>}\text{=}2A_3{\mu }_2-2A_3\beta u+A_4\beta u\mathrm{,}\\ A_{0v}\mathrm{<mo\; stretchy="false">(</mo>}u\mathrm{,}v\mathrm{<mo\; stretchy="false">)</mo>}\text{=}-\beta u{A}_1\mathrm{<mo\; stretchy="false">(</mo>}u\mathrm{,}v+\beta u{A}_2\mathrm{<mo\; stretchy="false">(</mo>}u\mathrm{,}v\mathrm{<mo\; stretchy="false">)</mo>}+{\mu }_2{A}_1\mathrm{<mo\; stretchy="false">(</mo>}u\mathrm{,}v\mathrm{<mo\; stretchy="false">)</mo>.}\end{array}\text{ (61)}$

Calculations give rise to,

$\begin{array}{c}{A}_2\mathrm{<mo\; stretchy="false">(</mo>}u\mathrm{,}v\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}v\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\left(B_1-A_4\beta u\right)+2A_{5}u\left(-\lambda +{\mu }_1+\lambda u+\beta v\right)+B_0\mathrm{,}\\ A_1\mathrm{<mo\; stretchy="false">(</mo>}u\mathrm{,}v\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{B}_2-A_5\beta u^2+2A_3{\mu }_{2}v-2A_3\beta uv+\frac{1}{2}{A}_{4}u(-2\lambda +2{\mu }_1\\ +2{\mu }_2+\beta u+2\lambda u+2\beta v\mathrm{<mo\; stretchy="false">)</mo>}-B_{1}u\mathrm{,}\\ A_0\mathrm{<mo\; stretchy="false">(</mo>}u\mathrm{,}v\mathrm{<mo\; stretchy="false">)</mo>}\text{=}-C_0+B_2{\mu }_{2}v-2A_3{\mu }_2^2{v}^2+\frac{1}{2}u\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}(2B_0\left(-\lambda +{\mu }_1+\lambda u+\beta v\right)\\ +2A_5({\lambda }^2{u}^3-2\lambda \left(\lambda -{\mu }_1\right)u^2+2{\mu }_{2}v\left(-\lambda +{\mu }_1+\beta v\right)\\ +u\left({\lambda }^2-2\lambda {\mu }_1+{\mu }_1^2-{\beta }^2{v}^2-{\mu }_2\mathrm{<mo\; stretchy="false">(</mo>}\beta -2\lambda \mathrm{<mo\; stretchy="false">)</mo>}v\right))\\ +\beta v\left(2A_5{\mu }_{2}u+2A_{3}v\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\left(\beta u-2{\mu }_2\right)-2B_2\right))\mathrm{.}\end{array}\text{ (62)}$

From (79) into (76) leads to,

$\begin{array}{c}+A_5{u^{\prime }}^2+A_4{u}^{\prime }{v}^{\prime }+A_3{v^{\prime }}^2+B_2{\mu }_{2}v-2A_3{\mu }_2^2{v}^2+u(B_0\left(-\lambda +{\mu }_1+\lambda u+\beta v\right)+\\ \beta v\left(A_{3}v\left(\beta u-2{\mu }_2\right)-B_2\right)+A_5-\lambda +{\mu }_1+\lambda u+\beta v(\lambda u^2+2{\mu }_{2}v\\ -u\left(\lambda -{\mu }_1+\beta v\right)))u^{\prime }\\ +\left(v\left(B_1-A_4\beta u\right)+2A_{5}u\left(-\lambda +{\mu }_1+\lambda u+\beta v\right)+B_0\right)\\ +\frac{1}{2}(2B_2-2B_1\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}-2A_5\beta u^2+4A_{3}v\left({\mu }_2-\beta u\right)+\\ A_{4}u\left(-2\lambda +2{\mu }_1+2{\mu }_2+\beta u+2\lambda u+2\beta v\right))v^{\prime }-C_0\mathrm{<mo>=</mo>0.}\end{array}\text{ (63)}$

Eq. (80) can be written as a Hamiltonian function,

$H\mathrm{<mo\; stretchy="false">(</mo>}{u}^{\prime }\mathrm{,}{v}^{\prime }\mathrm{,}u\mathrm{,}v\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{C}_0\mathrm{.}\text{ (64)}$

Conclusion

In this study, the alpha-difference operator (a-DO) and difference integrals are introduced. We establish the fundamental analysis and discover that the a-DO is reversible. We further explore the “invariant” a-DO-exponential function, along with trigonometric and hyperbolic functions. As a result, the a-difference forms a closed calculus, analogous to the q-calculus. We apply the a-DO to the logistic and prey-predator models with harvesting, focusing on the effects of varying the parameters. In the first case, we observe a critical time (t=1) at which the population distribution changes its behavior, transitioning from a growing state to a decaying one. The same results hold for the prey-predator model. Another typical example is the exposed-infected-recovery system. We find exact solutions for the linear fractional difference dynamic system. In the nonlinear case, we obtain approximate solutions by implementing an iterative scheme, for which we prove a convergence theorem. Furthermore, we construct the Hamiltonian function for the prey-predator system using a quadratic invariant. This provides further insights into the energy conservation and stability properties of the system. Our research opens up new avenues for the application of the a-DO in various fields of science and engineering.

Declarations

Data availability: Data sharing is not applicable to this paper as no data sets were generated or analyzed during the current study.

Conflicts of interest: The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Credit authorship contribution statement: H. I. Abdel-Gawad: Formal analysis, Methodology, Project administration, Writing - Original draft.

Ahmed. H. Abdel-Gawad: Formal analysis, Consulting, Writing - Revision.